Question

已知点集A={（x，y）|x²+y²-4x-8y+16≤0}，B={（x，y）|y≥|x-m|+4，m是常数}，点集A所表示的平面区域与点集B所表示的平面区域的边界的交点为M，N．若点D（m，4）在点集A所表示的平面区域内（不在边界上），则△DMN的面积的最大值是（ ）
A．1
B．2
C．
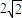
D．4

Answer 1

【答案】分析：先确定点D在直线y=4上，集合A表示的平面区域是图中圆O′的内部，集合B表示的平面区域是图中直角的内部，由此可得结论．
解答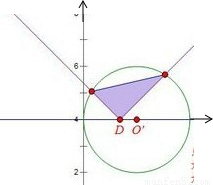：解：由题意，点D在直线y=4上，集合A表示的平面区域是图中圆O′的内部，集合B表示的平面区域是图中直角的内部
当D运动到O′时，△DMN的面积的最大值，此时三角形是一个直角边为2的等腰直角三角形，
所以面积为2
故选B．
点评：本题考查图形面积的计算，考查平面区域的确定，正确确定平面区域是关键．