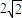题目内容
已知点集A={（x，y）|（x-3）2+（y-4）2≤（
）2}，B={（x，y）|（x-4）2+（y-5）2＞（
）2}，则点集A∩B中的整点（即横、纵坐标均为整数的点）的个数为
| 5 |
| 2 |
| 5 |
| 2 |
7
7
．分析：集合A表示圆心N（3，4），半径为
的圆上及圆内的点集，集合B表示圆心M（4，5），半径为
圆外的点集，A与B的交集即为图中红圆与绿园所夹的部分，由图形可得出交集点集中的整点个数．
| 5 |
| 2 |
| 5 |
| 2 |
解答：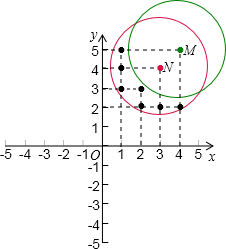
解：如图可知，点集A∩B中的整点为：（1，3），（1，4），（1，5），（2，2），（2，3），（3，2），（4，2）共7点．
故答案为：7
解：如图可知，点集A∩B中的整点为：（1，3），（1，4），（1，5），（2，2），（2，3），（3，2），（4，2）共7点．故答案为：7
点评：此题考查了点与圆的位置关系，利用了数形结合的思想，根据题意画出相应的图形是解本题的关键．
练习册系列答案
相关题目
）2}，B={（x，y）|（x-4）2+（y-5）2＞（
）2}，则点集A∩B中的整点（即横、纵坐标均为整数的点）的个数为 ．