题目内容
在平面直角坐标系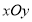
中，已知直线
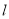的参数方程为
（
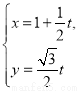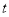为参数），椭圆
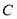的参数方程为
（
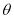为参数）．
（1）将直线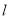
的参数方程化为极坐标方程；
（2）设直线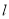
与椭圆
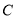相交于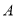
，
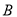两点，求线段
的长．
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
在平面直角坐标系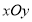中，已知直线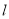的参数方程为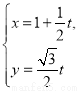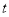（为参数），椭圆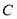的参数方程为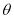（为参数）．
（1）将直线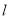的参数方程化为极坐标方程；
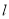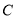（2）设直线与椭圆相交于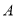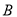，两点，求线段的长．
阅读快车系列答案
，若从区间[2,4]上任取一个数
，则所选取的实数
满足
的概率为（ ）
B．
D．
，
满足不等式组
且
的最小值为
，最大值为
，则
（ ）
B．
D．
在点
处的切线方程为
，则
．
，
，若
，则
（ ）
C．
D．
．
的最小正周期及单调递增区间；
时，函数
的最大值与最小值的和为
，求实数
的值．
若
，
，则关于
的方衡
的解的个数为（ ）
对
，不等式
恒成立；
，使不等式
成立，若
是真命题，
是假命题，求
的取值范围．