题目内容
记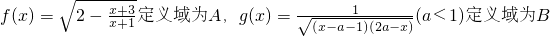 .
.
(1)求集合A
(2)若B⊆A,求a的范围
解:(1)要使函数有意义,则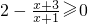 ,即
,即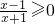 ,解得x≥1或x<-1,
,解得x≥1或x<-1,
故A={x|x≥1或x<-1};
(2)要使函数有意义,则(x-a-1)(2a-x)>0,即(x-a-1)(x-2a)<0,
∵a<1,∴2a<a+1,即2a<x<a+1,
∴B={x|2a<x<a+1},
∵B⊆A,∴a+1≤-1或2a≥1,解得a≤-2或a≥ ,
,
故a的范围是a≤-2或 ≤a<1.
≤a<1.
分析:(1)由偶次被开方数大于等于零,列出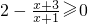 ,通分后求不等式的解集,就是函数的定义域A;
,通分后求不等式的解集,就是函数的定义域A;
(2)由偶次被开方数大于等于零和分母不为零,列出(x-a-1)(2a-x)>0,根据a<1求出不等式的解集,就是定义域B,再根据子集的定义列出关于a的不等式,求出a的范围,最后注意要与a<1求公共部分.
点评:本题考查了求函数的定义域和子集的定义,根据偶次被开方数大于等于零和分母不为零,分别求出函数的定义域,含有参数的不等式需要对端点值比较大小,根据子集定义求解时注意端点值的关系.
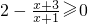 ,即
,即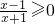 ,解得x≥1或x<-1,
,解得x≥1或x<-1,故A={x|x≥1或x<-1};
(2)要使函数有意义,则(x-a-1)(2a-x)>0,即(x-a-1)(x-2a)<0,
∵a<1,∴2a<a+1,即2a<x<a+1,
∴B={x|2a<x<a+1},
∵B⊆A,∴a+1≤-1或2a≥1,解得a≤-2或a≥
 ,
,故a的范围是a≤-2或
 ≤a<1.
≤a<1.分析:(1)由偶次被开方数大于等于零,列出
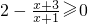 ,通分后求不等式的解集,就是函数的定义域A;
,通分后求不等式的解集,就是函数的定义域A;(2)由偶次被开方数大于等于零和分母不为零,列出(x-a-1)(2a-x)>0,根据a<1求出不等式的解集,就是定义域B,再根据子集的定义列出关于a的不等式,求出a的范围,最后注意要与a<1求公共部分.
点评:本题考查了求函数的定义域和子集的定义,根据偶次被开方数大于等于零和分母不为零,分别求出函数的定义域,含有参数的不等式需要对端点值比较大小,根据子集定义求解时注意端点值的关系.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目