题目内容
用适当的符号填空
(1)
(2)
+
},
(3){x|
=x,x∈R}
(1)
| 3 |
∈
∈
(1,2);(1,2)∈
∈
{(x,y)|y=x+1}(2)
| 2 |
| 5 |
∈
∈
{x|x≤2+| 3 |
(3){x|
| 1 |
| x |
⊆
⊆
{x|x3-x=0}.分析:(1)分析
与区间的关系是元素与集合的关系,根据
与区间端点的关系,易得到答案,由(1,2)表示一个点,而{(x,y)|y=x+1}表示一个点集,将点(1,2)的坐标代入验证即可得到答案.
(2)分析数
+
与2+
的大小关系,即可得到答案;
(3)根据两边均为集合的形式,分析解方程得到两边集合的列举法表示方式,进而根据集合关系的判定方法易得到答案.
| 3 |
| 3 |
(2)分析数
| 2 |
| 5 |
| 3 |
(3)根据两边均为集合的形式,分析解方程得到两边集合的列举法表示方式,进而根据集合关系的判定方法易得到答案.
解答:解:(1)
≤2,x=1,y=2满足y=x+1,
(2)估算
+
=1.4+2.2=3.6,2+
=3.7,或(
+
)2=7+
,(2+
)2=7+
(3)左边={-1,1},右边={-1,0,1}
| 3 |
(2)估算
| 2 |
| 5 |
| 3 |
| 2 |
| 5 |
| 40 |
| 3 |
| 48 |
(3)左边={-1,1},右边={-1,0,1}
点评:本题考查的知识点是元素与集合关系的判断,集合与集合关系的判断,其中分析符号两边进而选择恰当的符号来表示左右两边的关系是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,
,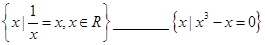
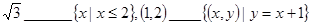
 ,
,