题目内容
下列四个函数:①
 ;
;②f(x)=2x;
③
 ;
;④
 .
.其中为奇函数的是 ;在(1,+∞)上单调递增的函数是 (分别填写所有满足条件的函数序号)
【答案】分析:利用奇函数和和函数的单调性的定义分别判断即可.
解答:解:①函数的定义域为{x|x≠0}关于原点对称,且 ,所以函数f(x)为奇函数.在(1,+∞)上单调递减.
,所以函数f(x)为奇函数.在(1,+∞)上单调递减.
②函数的定义域为R,函数f(x)=2x,为非奇非偶函数.此时函数在R上单调递增.
③函数的定义域为R,当x>0,f(-x)=-x2+3=-(x2-3)=-f(x),
当x<0时,f(-x)=x2-3=-(-x2+3)=-f(x),综上恒有f(-x)=-f(x),所以函数为奇函数.在(1,+∞)上单调递增.
④函数的定义域为R,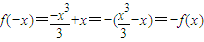 ,所以函数为奇函数.函数的导数为f'(x)=x2-1,当x>1时,f'(x)=x2-1>0,所以函数在(1,+∞)上单调递增.
,所以函数为奇函数.函数的导数为f'(x)=x2-1,当x>1时,f'(x)=x2-1>0,所以函数在(1,+∞)上单调递增.
故答案为:①③④;②③④.
点评:本题主要考查函数奇偶性的判断以及函数单调性的应用,要求熟练掌握相关的定义.
解答:解:①函数的定义域为{x|x≠0}关于原点对称,且
 ,所以函数f(x)为奇函数.在(1,+∞)上单调递减.
,所以函数f(x)为奇函数.在(1,+∞)上单调递减.②函数的定义域为R,函数f(x)=2x,为非奇非偶函数.此时函数在R上单调递增.
③函数的定义域为R,当x>0,f(-x)=-x2+3=-(x2-3)=-f(x),
当x<0时,f(-x)=x2-3=-(-x2+3)=-f(x),综上恒有f(-x)=-f(x),所以函数为奇函数.在(1,+∞)上单调递增.
④函数的定义域为R,
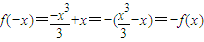 ,所以函数为奇函数.函数的导数为f'(x)=x2-1,当x>1时,f'(x)=x2-1>0,所以函数在(1,+∞)上单调递增.
,所以函数为奇函数.函数的导数为f'(x)=x2-1,当x>1时,f'(x)=x2-1>0,所以函数在(1,+∞)上单调递增.故答案为:①③④;②③④.
点评:本题主要考查函数奇偶性的判断以及函数单调性的应用,要求熟练掌握相关的定义.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目