题目内容
(文科选做)(2-5)+(4-52)+…(2n-5n)=
n(n+1)+
| 5(1-5n) |
| 4 |
n(n+1)+
.| 5(1-5n) |
| 4 |
分析:将数列和分成两个数列的和,然后利用等差数列及等比数列的前n项和公式求出和.
解答:解:(2-5)+(4-52)+…(2n-5n)
=(2+4+…+2n)-(5+52+…+5n)
=
-
=n(n+1)+
故答案为n(n+1)+
=(2+4+…+2n)-(5+52+…+5n)
=
| (2+2n)n |
| 2 |
| 5-5n+1 |
| 1-5 |
=n(n+1)+
| 5(1-5n) |
| 4 |
故答案为n(n+1)+
| 5(1-5n) |
| 4 |
点评:求数列的前n项和的问题,一般先求出数列的通项公式,根据通项公式的特点,选择合适的求和方法.常见的求和方法有:公式法、倒序相加法、错位相减法、裂项相消法、分组法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
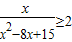 .
.