题目内容
1、f(x)在x=x0处连续是f(x)在x=x0处有定义的( )条件.
分析:由题意看命题f(x)在x=x0处连续与命题f(x)在x=x0处有定义是否能互推,然后根据必要条件、充分条件和充要条件的定义进行判断.
解答:解:∵f(x)在x=x0处有定义不一定连续,
∴f(x)在x=x0处连续?f(x)在x=x0处有定义,
反之则不可以,
∴f(x)在x=x0处连续是f(x)在x=x0处有定义的充分不必要条件,
故选A.
∴f(x)在x=x0处连续?f(x)在x=x0处有定义,
反之则不可以,
∴f(x)在x=x0处连续是f(x)在x=x0处有定义的充分不必要条件,
故选A.
点评:此题主要考查函数连续和有定义的关系及必要条件、充分条件和充要条件的定义,是一道基础题.

练习册系列答案
相关题目
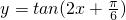 在区间
在区间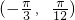 上单调递增;
上单调递增;