题目内容
 分别以双曲线G:
分别以双曲线G:| x2 |
| 2 |
| y2 |
| 2 |
(Ⅰ)求椭圆C的方程;
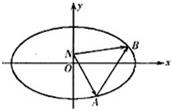
(Ⅱ)在y轴上是否存在点N(0,n),使得(
| NA |
| NB |
| AB |
分析:(I)依题意可设椭圆C的方程为
+
=1(a>b>0),a2=4,c2=2,b2=2.由此可知椭圆C的方程为
+
=1.
(II)椭圆C的右焦点为F(
,0),设直线l的方程为y=k(x-
),k≠0.由
得(1+2k2)x2-4
k2x+4k2-4=0.设A(x1,y1),B(x2,y2),记AB的中点为M(x0,y0),M(
,-
),由此入手能够推导出n的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 4 |
| y2 |
| 2 |
(II)椭圆C的右焦点为F(
| 2 |
| 2 |
|
| 2 |
2
| ||
| 1+2k2 |
| ||
| 1+2k2 |
解答: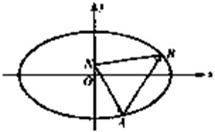 解:(I)依题意可设椭圆C的方程为
解:(I)依题意可设椭圆C的方程为
+
=1(a>b>0),
且a2=2+2+=4,c2=a2-b2=2,∴b2=2.(2分)
所以椭圆C的方程为
+
=1.(4分)
(II)椭圆C的右焦点为F(
,0),
设直线l的方程为y=k(x-
),k≠0.
由
得(1+2k2)x2-4
k2x+4k2-4=0.(6分)
设A(x1,y1),B(x2,y2),记AB的中点为M(x0,y0),
则x0=
=
,∴y0=k(x0-
)=-
,
∴M(
,-
),
若存在点N(0,n),使得(
+
)•
=0,
等价于存在点N(0,n),使得2
•
=0,
从而
•k=-1,(8分)
解得n=
=
.k≠0,
当k>0时,
+2k≥2
,当且仅当k=
时取等号.(10分)
当k<0时,
+2k=-[(-
)+(-2k)]≤-2
当且仅当k=-
时取等号.(11分)
所以存在点N(0,n),使得(
+
)•
=0.
且n的取值范围是[-
,0)∪(0,
].(14分)
 解:(I)依题意可设椭圆C的方程为
解:(I)依题意可设椭圆C的方程为| x2 |
| a2 |
| y2 |
| b2 |
且a2=2+2+=4,c2=a2-b2=2,∴b2=2.(2分)
所以椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 2 |
(II)椭圆C的右焦点为F(
| 2 |
设直线l的方程为y=k(x-
| 2 |
由
|
得(1+2k2)x2-4
| 2 |
设A(x1,y1),B(x2,y2),记AB的中点为M(x0,y0),
则x0=
| x1+x2 |
| 2 |
2
| ||
| 1+2k2 |
| 2 |
| ||
| 1+2k2 |
∴M(
2
| ||
| 1+2k2 |
| ||
| 1+2k2 |
若存在点N(0,n),使得(
| NA |
| NB |
| AB |
等价于存在点N(0,n),使得2
| NM |
| AB |
从而
-
| ||||
|
解得n=
| ||
| 1+2k2 |
| ||
|
当k>0时,
| 1 |
| k |
| 2 |
| ||
| 2 |
当k<0时,
| 1 |
| k |
| 1 |
| k |
| 2 |
当且仅当k=-
| ||
| 2 |
所以存在点N(0,n),使得(
| NA |
| NB |
| AB |
且n的取值范围是[-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查直线和椭圆的位置关系,解题时要认真审题,注意挖掘题设中的隐含条件,仔细解答.

练习册系列答案
相关题目
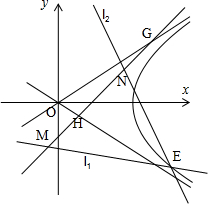
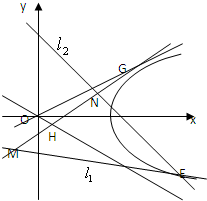
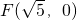 为右焦点的双曲线C的离心率
为右焦点的双曲线C的离心率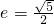 .
. .
.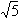 ,0)为右焦点的双曲线C的离心率
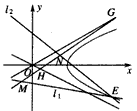
,0)为右焦点的双曲线C的离心率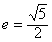 。
。
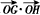 的值。
的值。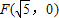 为右焦点的双曲线C的离心率
为右焦点的双曲线C的离心率 .
.
 为右焦点的双曲线C的离心率
为右焦点的双曲线C的离心率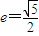 .
.