题目内容
下列三个说法不正确的个数是
①零向量是长度为0的向量,所以零向量与非零向量不平行.
②因为平面内的向量与这个平面内的有向线段一一对应,所以平面内的向量可以用这个平面内的有向线段表示.
③因为向量
∥
,所以AB∥CD.( )
①零向量是长度为0的向量,所以零向量与非零向量不平行.
②因为平面内的向量与这个平面内的有向线段一一对应,所以平面内的向量可以用这个平面内的有向线段表示.
③因为向量
| AB |
| CD |
| A、3 | B、2 | C、1 | D、0 |
分析:由零向量与任意向量都平行,可判断①的真假;由向量与有向量线段的关系可判断②的真假;由共线(平行)向量的几何特征,可判断③的真假,进而得到答案.
解答:解:零向量与任意向量都平行,故①错误;
有向量与有向量线段的关系可得,零向量无法用有向线段表示,故②错误;
当向量
∥
,AB与CD平行或共线,故③错误
故选A.
有向量与有向量线段的关系可得,零向量无法用有向线段表示,故②错误;
当向量
| AB |
| CD |
故选A.
点评:本题考查的知识点是零向量,向量的几何表示,其中在向量问题中一定要注意零向量的特殊性.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
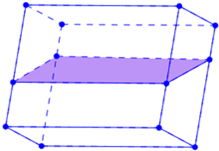 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内装进一些水,将容器底面一边BC固定于底面上,再将容器倾斜,随着倾斜度的不同,有下列三个说法:①水的形状始终是棱柱形状;②水面形成的四边形EFGH的面积不改变;③当E∈AA1时,AE+BF是定值.其中正确说法是
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内装进一些水,将容器底面一边BC固定于底面上,再将容器倾斜,随着倾斜度的不同,有下列三个说法:①水的形状始终是棱柱形状;②水面形成的四边形EFGH的面积不改变;③当E∈AA1时,AE+BF是定值.其中正确说法是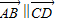 ,所以AB∥CD.( )
,所以AB∥CD.( )