题目内容
求与椭圆 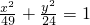 有公共焦点,且离心率是
有公共焦点,且离心率是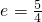 的双曲线方程,并求其渐近线方程.
的双曲线方程,并求其渐近线方程.
解:椭圆 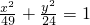 中c=
中c=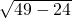 =5,
=5,
∵双曲线与椭圆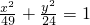 有公共焦点,且离心率是
有公共焦点,且离心率是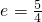
∴c=5,a=4,
∴b2=25-16=9
∴双曲线方程为: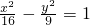
其渐近线方程为: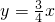 .
.
分析:先求出双曲线的几何量,可得双曲线的标准方程,即可求其渐近线方程.
点评:本题考查椭圆、双曲线的标准方程,考查学生的计算能力,属于基础题.
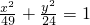 中c=
中c=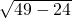 =5,
=5,∵双曲线与椭圆
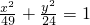 有公共焦点,且离心率是
有公共焦点,且离心率是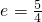
∴c=5,a=4,
∴b2=25-16=9
∴双曲线方程为:
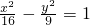
其渐近线方程为:
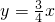 .
.分析:先求出双曲线的几何量,可得双曲线的标准方程,即可求其渐近线方程.
点评:本题考查椭圆、双曲线的标准方程,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
 有公共焦点,且离心率为2的双曲线方程.
有公共焦点,且离心率为2的双曲线方程. 有公共焦点,且一条渐近线为
有公共焦点,且一条渐近线为 的双曲线的方程.
的双曲线的方程. 有公共焦点,且离心率
有公共焦点,且离心率 的双曲线的方程.
的双曲线的方程. 有公共焦点,且离心率为2的双曲线方程.
有公共焦点,且离心率为2的双曲线方程.