题目内容
求与椭圆 有公共焦点,且离心率为2的双曲线方程.
有公共焦点,且离心率为2的双曲线方程.
解:椭圆 的焦点坐标为(-4,0)和(4,0)
的焦点坐标为(-4,0)和(4,0)
设双曲线方程
则
∴a=2,b2=c2-a2=12,
∴所求双曲线方程为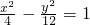 .
.
分析:根据题意可得: ,进而求出a,b的数值即可求出双曲线的方程.
,进而求出a,b的数值即可求出双曲线的方程.
点评:本题主要考查双曲线的标准方程,以及双曲线的有关性质.
 的焦点坐标为(-4,0)和(4,0)
的焦点坐标为(-4,0)和(4,0)设双曲线方程

则

∴a=2,b2=c2-a2=12,
∴所求双曲线方程为
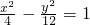 .
.分析:根据题意可得:
 ,进而求出a,b的数值即可求出双曲线的方程.
,进而求出a,b的数值即可求出双曲线的方程.点评:本题主要考查双曲线的标准方程,以及双曲线的有关性质.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 有公共焦点,且一条渐近线为
有公共焦点,且一条渐近线为 的双曲线的方程.
的双曲线的方程. 有公共焦点,且离心率
有公共焦点,且离心率 的双曲线的方程.
的双曲线的方程. 有公共焦点,且离心率为2的双曲线方程.
有公共焦点,且离心率为2的双曲线方程.