题目内容
若直线y=x是曲线y=x3-3x2+ax-1的切线,则a的值为 .
【答案】分析:设出直线y=x与曲线y=x3-3x2+ax-1的切点,求出曲线在切点处的导数值,由导数值等于1列一个关于切点横坐标和a的方程,再由切点在直线y=x上得另一方程,两个方程联立可求a的值.
解答:解:由y=x3-3x2+ax-1,得:y′=3x2-6x+a.
设直线y=x与曲线y=x3-3x2+ax-1切于(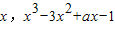 ),
),
又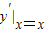 =
=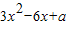 ,所以,
,所以,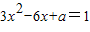 ①
①
由(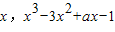 )在直线y=x上,
)在直线y=x上,
∴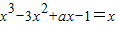 ②
②
由①得,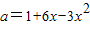 ③
③
把③代入②得: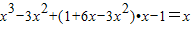
整理得: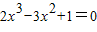 ,
,
即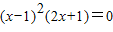 ,
,
所以,x=1或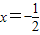 .
.
当x=1时,a=1+6×1-3×12=4.
当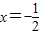 时,a=
时,a=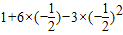 =
=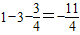 .
.
所以a的值为4或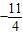 .
.
故答案为4或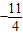 .
.
点评:本题考查了利用导数研究曲线上某点的切线方程,函数在某点处的导数,就是对应曲线上在该点处的切线的斜率,考查了利用因式分解求解一元三次方程.此题是中档题.
解答:解:由y=x3-3x2+ax-1,得:y′=3x2-6x+a.
设直线y=x与曲线y=x3-3x2+ax-1切于(
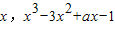 ),
),又
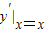 =
=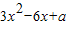 ,所以,
,所以,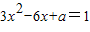 ①
①由(
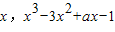 )在直线y=x上,
)在直线y=x上,∴
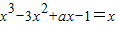 ②
②由①得,
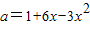 ③
③把③代入②得:
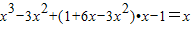
整理得:
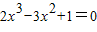 ,
,即
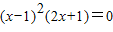 ,
,所以,x=1或
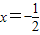 .
.当x=1时,a=1+6×1-3×12=4.
当
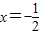 时,a=
时,a=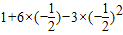 =
=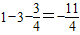 .
.所以a的值为4或
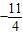 .
.故答案为4或
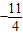 .
.点评:本题考查了利用导数研究曲线上某点的切线方程,函数在某点处的导数,就是对应曲线上在该点处的切线的斜率,考查了利用因式分解求解一元三次方程.此题是中档题.

练习册系列答案
相关题目
若直线y=x是曲线y=x3-2x2+ax的切线,则a=( )
| A、1 | B、2 | C、-1 | D、1或2 |