题目内容
一袋中装有分别标记着1、2、3、4 数字的4个球, 从这只袋中每次取出1个球, 取出后放回, 连续取三次, 设三次取出的球中数字最大的数为ξ.(1) 求ξ=3时的概率; (2) 求ξ的概率分布列及数学期望.
(1)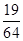 (2)
(2)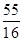
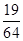 (2)
(2)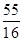
【错解分析】概率、分布列、期望和方差的计算。突破此难点的关键在于:首先要运用两个基本原理认真审题,弄清楚问题属于四种类型事件中的哪一种,然后准确地运用相应的公式进行计算,其中要注意排列、组合知识的应用。
【正解】本题主要考查随机变量的分布列和期望,考查限制条件下的概率计算.处理离散型变量时,注意正确判断随机变量的取值,全面剖析各个随机变量所包含的各种事件及相互关系,准确计算变量的每个取值的概率。
(1) ξ=3表示取出的三个球中数字最大者为3
①三次取球均出现最大数字为3的概率 P1=
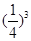
②三取取球中有2次出现最大数字3的概率
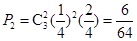
③三次取球中仅有1次出现最大数字3的概率
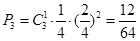
三次取出的球中数字最大的数为3的概率

(2) 在ξ=k时, 利用(1)的原理可知:


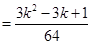 (k="1,2,3,4)." ξ 的概率分布列为:
(k="1,2,3,4)." ξ 的概率分布列为: | ξ | 1 | 2 | 3 | 4 |
| P | 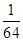 | 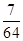 | 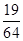 |  |
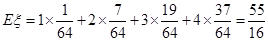

练习册系列答案
相关题目
 )获得身高数据的茎叶图如下:
)获得身高数据的茎叶图如下: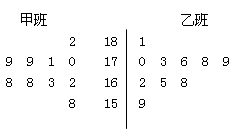
 的同学,求至少有一名身高大于
的同学,求至少有一名身高大于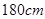 的同学被抽中的概率。
的同学被抽中的概率。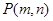 落在圆x2+y2=16内的概率是.
落在圆x2+y2=16内的概率是.
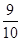
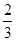
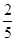
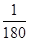
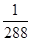
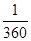


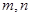 作为点
作为点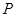 的坐标,则点
的坐标,则点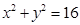 内的概率为( )
内的概率为( )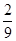
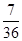
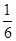
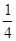
 张卡片(大小,形状都相同)上分别写有
张卡片(大小,形状都相同)上分别写有 ,
, ,
,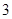 ,
,