题目内容
例4.已知数列{an}中,a1=3,对于nN,以an,an+1为系数的一元二次方程anx2-2 an+1x+1=0都有根α、β且满足(α-1)(β-1)=2.
(1)求证数列
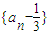 是等比数列.
是等比数列.(2)求数列{an}的通项公式.
【答案】分析:(1)根据韦达定理可知α+β=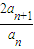 ,αβ=
,αβ= ,代入(α-1)(β-1)=2中整理得an-
,代入(α-1)(β-1)=2中整理得an- =-2(an+1-
=-2(an+1- ),进而可判定数列
),进而可判定数列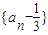 是等比数列.
是等比数列.
(2)由(1)可求得数列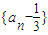 的首项和公比,可求得数列
的首项和公比,可求得数列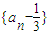 的通项公式,进而求得an.
的通项公式,进而求得an.
解答:解:(1)证明:依题意可知α+β= ,αβ=
,αβ=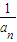
∴(α-1)(β-1)=αβ-(α+β)+1=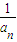 -
-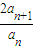 +1=2
+1=2
整理得an- =-2(an+1-
=-2(an+1- ),a1-
),a1- =
=
∴数列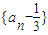 是以
是以 为首项,-
为首项,- 为公比的等比数列.
为公比的等比数列.
(2)由(1)知an- =
= ×(-
×(- )n-1,
)n-1,
∴an= ×(-
×(- )n-1+
)n-1+ .
.
点评:本题主要考查了等比数列的性质和等比关系的确定.考查了学生对等比数列的定义和通项公式的理解和把握.
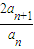 ,αβ=
,αβ= ,代入(α-1)(β-1)=2中整理得an-
,代入(α-1)(β-1)=2中整理得an- =-2(an+1-
=-2(an+1- ),进而可判定数列
),进而可判定数列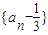 是等比数列.
是等比数列.(2)由(1)可求得数列
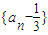 的首项和公比,可求得数列
的首项和公比,可求得数列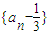 的通项公式,进而求得an.
的通项公式,进而求得an.解答:解:(1)证明:依题意可知α+β=
 ,αβ=
,αβ=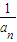
∴(α-1)(β-1)=αβ-(α+β)+1=
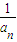 -
-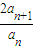 +1=2
+1=2整理得an-
 =-2(an+1-
=-2(an+1- ),a1-
),a1- =
=
∴数列
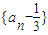 是以
是以 为首项,-
为首项,- 为公比的等比数列.
为公比的等比数列.(2)由(1)知an-
 =
= ×(-
×(- )n-1,
)n-1,∴an=
 ×(-
×(- )n-1+
)n-1+ .
.点评:本题主要考查了等比数列的性质和等比关系的确定.考查了学生对等比数列的定义和通项公式的理解和把握.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 最大时,求n的值.
最大时,求n的值.