题目内容
例4:已知数列{an}首项a1>1,公比q>0的等比数列,设bn=log2an(n∈N*),且b1+b3+b5=6,b1b3b5=0,记{bn}的前n项和为Sn,当| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
分析:先根据b1+b3+b5=6及bn=log2an,求得a3的值,再根据b1b3b5=0,则a1a3a5必有一个是1,a1>1,a3=4分析得a5=1,进而可求得数列{an}的通项公式,代入bn=log2an中求得{bn}的通项公式.要使
+
+…+
最大即求使
≥0的最后一项,进而可得答案.
| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
| Sn |
| n |
解答:解:∵b1+b3+b5=6,
∴log2a1+log2a3+log2a5=log2(a1a3a5)=log23a36
解得a3=4
∵b1b3b5=0,则a1a3a5必有一个是1
∵a1>1 a3=4
∴a5=1
由a3和a5易得an=2(5-n)
∴bn=5-n
Sn=
=
要使
+
+…+
最大
即求使
≥0的最后一项
易得n为8或9
∴log2a1+log2a3+log2a5=log2(a1a3a5)=log23a36
解得a3=4
∵b1b3b5=0,则a1a3a5必有一个是1
∵a1>1 a3=4
∴a5=1
由a3和a5易得an=2(5-n)
∴bn=5-n
Sn=
| n(b1+bn) |
| 2 |
| (9-n)n |
| 2 |
要使
| S1 |
| 1 |
| S2 |
| 2 |
| Sn |
| n |
即求使
| Sn |
| n |
易得n为8或9
点评:本题主要考查了等比数列的性质.涉及了数列的最值问题.属中档题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 最大时,求n的值.
最大时,求n的值.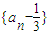 是等比数列.
是等比数列.