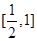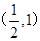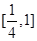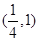题目内容
已知点A(0, –1),点B在直线x–y+1=0上,直线AB垂直于直线x+2y–3=0,则点B的坐标是( )
| A.(–2, –3) | B.(2, 3) | C.(2, 1) | D.(–2, 1) |
B
解析试题分析:因为直线AB垂直于直线x+2y–3=0,所以直线AB的斜率为2,由直线方程的点斜式得AB的方程为y=2x-1与x–y+1=0联立可得点B的坐标是(2, 3),故选B。
考点:本题主要考查直线的一般式方程与直线的垂直关系,方程组解法.
点评:基础题,根据两直线垂直,要么斜率相乘等于-1,要么一条直线斜率不存在,另一条斜率为0。先确定直线AB的方程,再求交点坐标。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆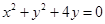 与直线
与直线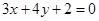 相交于A、B两点,则线段AB的垂直平分线的方程是( )
相交于A、B两点,则线段AB的垂直平分线的方程是( )
A.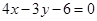 | B.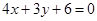 |
C.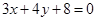 | D.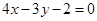 |
如果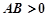 ,
,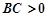 ,那么直线
,那么直线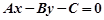 不经过的象限是 ( )
不经过的象限是 ( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
若直线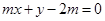 与直线
与直线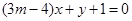 垂直,则
垂直,则 的值是( )
的值是( )
A.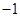 或 或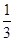 | B.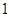 或 或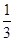 | C.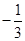 或 或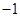 | D.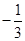 或1 或1 |
倾斜角为135°,在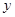 轴上的截距为
轴上的截距为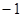 的直线方程是( )
的直线方程是( )
A.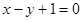 | B.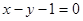 |
C.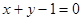 | D.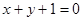 |
经过两点(3,9)、(-1,1)的直线在x轴上的截距为
A.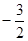 | B.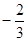 | C.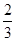 | D.2 |
( )由直线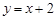 上的一点向圆
上的一点向圆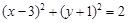 引切线,则切线长的最小值为
引切线,则切线长的最小值为
A.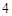 | B.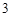 | C.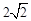 | D. |
两直线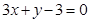 与
与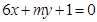 平行,则它们之间的距离为( )
平行,则它们之间的距离为( )
A.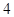 | B. | C.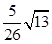 | D.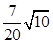 |
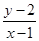 的取值范围是
的取值范围是