题目内容
设 ,
,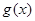 分别是定义在
分别是定义在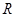 上的奇函数和偶函数,当
上的奇函数和偶函数,当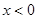 时,
时,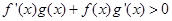 ,且
,且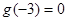 ,则不等式
,则不等式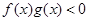 的解集是 ( )
的解集是 ( )
A. | B.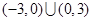 |
C. | D.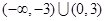 |
D.
解析试题分析:先根据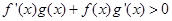 可确定
可确定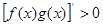 ,进而可得到
,进而可得到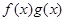 在
在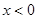 时单调递增,结合函数
时单调递增,结合函数 ,
,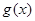 分别是定义在
分别是定义在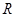 上的奇函数和偶函数可确定
上的奇函数和偶函数可确定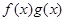 在
在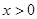 时也是增函数.于是构造函数
时也是增函数.于是构造函数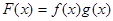 知
知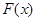 在
在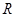 上为奇函数且为单调递增的,又因为
上为奇函数且为单调递增的,又因为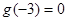 ,所以
,所以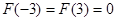 ,所以
,所以 的解集为
的解集为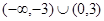 ,故选D.
,故选D.
考点:利用导数研究函数的单调性.

练习册系列答案
相关题目
曲线 在横坐标为
在横坐标为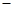 l的点处的切线为
l的点处的切线为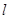 ,则点P(3,2)到直线
,则点P(3,2)到直线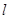 的距离为( )
的距离为( )
A.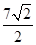 | B.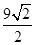 | C.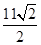 | D.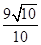 |
已知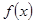 为定义在(-
为定义在(-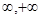 )上的可导函数,
)上的可导函数,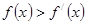 对于
对于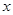 ∈R恒成立,且e为自然对数的底数,则( )
∈R恒成立,且e为自然对数的底数,则( )
A.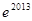 . .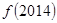 < < . .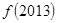 |
B.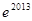 . .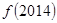 = = . .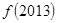 |
C.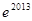 . .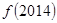 > > . .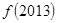 |
D.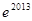 . .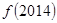 与 与 . .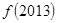 大小不确定 大小不确定 |
若函数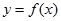 在区间
在区间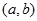 内可导,且
内可导,且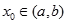 ,则
,则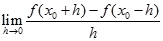
的值为( )
A.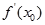 | B.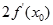 | C. | D.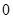 |
已知函数 ,若曲线
,若曲线 存在与直线
存在与直线 平行的切线,则实数
平行的切线,则实数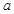 的取值范围是( )
的取值范围是( )
A.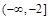 | B. | C.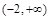 | D.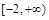 |
观察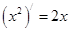 ,
,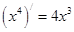 ,
,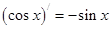 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在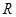 上的函数
上的函数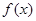 满足
满足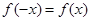 ,记
,记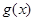 为
为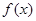 的导函数,则
的导函数,则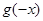 =( )
=( )
A.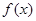 | B.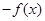 | C.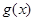 | D.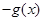 |
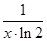 ;③(ex)′=ex;④(
;③(ex)′=ex;④(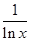 )′=x;⑤(x·ex)′=ex+1.
)′=x;⑤(x·ex)′=ex+1. 的图象如图所示,若
的图象如图所示,若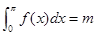 ,则
,则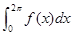 等于( )
等于( )
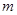 B.2m C.0 D.-m
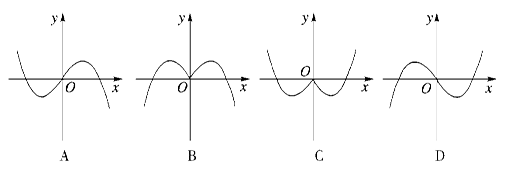
B.2m C.0 D.-m 的导函数原点处的部分图象大致为 ( )
的导函数原点处的部分图象大致为 ( )