题目内容
(19)如图,椭圆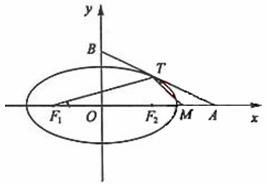
(Ⅰ)求椭圆方程;
(Ⅱ)设F1、F2分别为椭圆的左、右焦点,M为线段AF2的中点,求证:∠ATM=∠AF1T。
本题主要考查直线与椭圆的位置关系、椭圆的几何性质,同时考查解析几何的基本思想方法和综合解题能力。
解:(Ⅰ)过点A、B的直线方程为![]() .
.
因为由题意得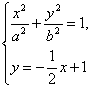 有惟一解,
有惟一解,
即![]() 有惟一解,
有惟一解,
所以
△=![]() (ab≠0),
(ab≠0),
故 ![]() ,
,
又因为![]() ,即
,即![]() ,
,
所以![]()
从而得![]() ,
,
故所求的椭圆方程为 ![]() 。
。
(Ⅱ)由(Ⅰ)得![]() ,
,
故![]()
从而M![]()
由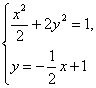 解得
解得![]()
所以T(1,![]() ).
).
因为![]() ,
,
又![]() ,得
,得
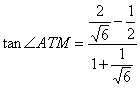
=![]()
因此![]()

练习册系列答案
相关题目
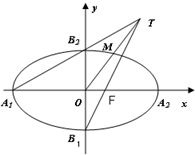 如图,在平面直角坐标系xoy中,A1,A2,B1,B2为椭圆
如图,在平面直角坐标系xoy中,A1,A2,B1,B2为椭圆
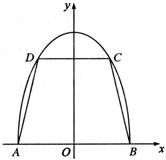
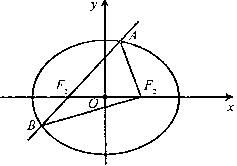 如图,椭圆
如图,椭圆