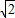Question

已知直线bx+ay=ab与圆x²+y²=1相切，若a，b同号，则ab的最小值为（　　）

• A、1
• B、2
• C、

  2

• D、不存在

Answer 1

分析：先用原点到直线的距离等于半径，得到a、b的关系，再用基本不等式确定ab的范围．

解答：解：已知直线bx+ay=ab与圆x²+y²=1相切，则

1

a2

+

1

b2

=1．
由于a，b同号，则ab的最小值为2，
故选B．

点评：本题考查直线与圆的位置关系，基本不等式，此式a2+b2≥2|ab|是易出错点，本题是考查学生能力的小题．