题目内容
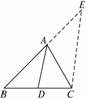
如图1-2-9,已知AD是△ABC的内角平分线,求证:
图1-2-9
思路分析:AB、AC不在同一直线上,而BD和CD在同一直线上.在同一直线上的两条线段的比往往和平行线有关,所以我们考虑不妨作一条平行线.
证明:过点C作CE∥AD,交BA的延长线于点E,
∵AD∥EC,∴![]()
又∵∠E=∠BAD,∠CAD=∠ACE,∠BAD=∠CAD,
∴∠E=∠ACE.∴AC=AE.∴![]() .
.
深化升华 此题是三角形的内角平分线定理,即三角形的内角平分线分对边成两条线段与夹这个角的两边对应成比例.

练习册系列答案
相关题目