题目内容
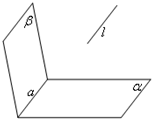已知：直线l∥平面α，直线l∥平面β，且α∩β=a，求证：l∥a．分析：分别过直线l作两个平面，分别和α，β相交，得到两条交线，利用线面平行的性质定理和直线平行的传递性证明l∥a．
解答：
证明：过直线l分别作两个辅助平面交α，β与m，n．
因为直线l∥平面α，所以l∥m．
直线l∥平面β，所以l∥n．
则m∥n，所以m∥α．
因为α∩β=a，所以m∥a，
所以l∥a．
证明：过直线l分别作两个辅助平面交α，β与m，n．因为直线l∥平面α，所以l∥m．
直线l∥平面β，所以l∥n．
则m∥n，所以m∥α．
因为α∩β=a，所以m∥a，
所以l∥a．
点评：本题主要考查了线面平行的判断和性质定理，以及利用直线平行的平行公理证明直线平行，作两个辅助平面，是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目