题目内容
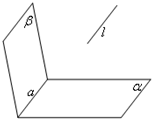
已知:直线l⊥平面α,直线m?平面β,下面四个命题正确的是( )A.α∥β⇒l与m异面
B.l∥m⇒α⊥β
C.α⊥β⇒l∥m
D.l⊥m⇒α∥β
【答案】分析:由题意,直线l⊥平面α,直线m?平面β,依次对四个选项中的命题进行判断,得出正确选项即可,A选项由线线的位置关系判断,B选项由面面垂直的条件判断,C选项由线面平行的条件判断,D选项由面面平行的条件判断.
解答:解:由题意知直线l⊥平面α,直线m?平面β,
考察A选项,此选项中的命题不正确,因为根据α∥β可得出l⊥平面β,由于不能排除l与m相交的情况,故得不出两线异面的结论;
考察B选项,此选项中的命题正确,由题设条件知,l∥m可得出m⊥平面α,又直线m?平面β 故可得α⊥β
考察C选项,此选项中的命题错误,由α⊥β及直线l⊥平面α,可得,l∥β或直线l?平面β,故l与m相交、平行异面都有可能;
考察D选项,此选项错误,因为l⊥m,线l⊥平面α可得m∥α或直线m?平面α,故两平面相交平行都有可能,所以不正确,
综上,B选项中的命题是正确的
故选B
点评:本题考点是面面垂直的判定,考查了线线异面的判断,面面垂直的判定,线面平行的判定,面面平行的判定,解题的关键是有着较强的空间想像能力,且能根据图形及所给的条件作出正确判断,本题考查了空间想像能力,推理判断的能力,此类题型是近几年高考中经常出现的题型,由于其考查的知识点多,容量大,尤其被命题者偏爱
解答:解:由题意知直线l⊥平面α,直线m?平面β,
考察A选项,此选项中的命题不正确,因为根据α∥β可得出l⊥平面β,由于不能排除l与m相交的情况,故得不出两线异面的结论;
考察B选项,此选项中的命题正确,由题设条件知,l∥m可得出m⊥平面α,又直线m?平面β 故可得α⊥β
考察C选项,此选项中的命题错误,由α⊥β及直线l⊥平面α,可得,l∥β或直线l?平面β,故l与m相交、平行异面都有可能;
考察D选项,此选项错误,因为l⊥m,线l⊥平面α可得m∥α或直线m?平面α,故两平面相交平行都有可能,所以不正确,
综上,B选项中的命题是正确的
故选B
点评:本题考点是面面垂直的判定,考查了线线异面的判断,面面垂直的判定,线面平行的判定,面面平行的判定,解题的关键是有着较强的空间想像能力,且能根据图形及所给的条件作出正确判断,本题考查了空间想像能力,推理判断的能力,此类题型是近几年高考中经常出现的题型,由于其考查的知识点多,容量大,尤其被命题者偏爱

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 已知:直线l∥平面α,直线l∥平面β,且α∩β=a,求证:l∥a.
已知:直线l∥平面α,直线l∥平面β,且α∩β=a,求证:l∥a.