题目内容
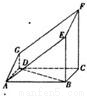
 如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.(I)求证:BD⊥平面ADG;
(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的大小.
分析:(I)由已知中多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形,由勾股定理可得AD⊥BD,由直平行六面体的几何特征,可得GD⊥BD,由线面垂直的判定定理,可得BD⊥平面ADG;
(Ⅱ)以D为坐标原点,建立如图所示的空间直角坐标系D-xyz,分别求出平面AEFG和平面ABCD的一个法向量,代入向量的夹角公式,即可求出平面AEFG与平面ABCD所成锐二面角的大小.
(Ⅱ)以D为坐标原点,建立如图所示的空间直角坐标系D-xyz,分别求出平面AEFG和平面ABCD的一个法向量,代入向量的夹角公式,即可求出平面AEFG与平面ABCD所成锐二面角的大小.
解答:解:(I)证明:在△BAD中,∵AB=2AD=2,∠BAD=60°
∴由余弦定理,可得BD=
∴AB2=AD2+BD2,∴AD⊥BD
又在直平行六面体中,GD⊥平面ABCD,∴GD⊥BD
又AD∩GD=D,∴BD⊥平面ADG(5分)
(Ⅱ)以D为坐标原点,建立如图所示的空间直角坐标系D-xyz
∵∠BAE=∠GAD=45°,AB=2AD=2
则有A(1,0,0),B(0,
,0),G(0,0,1),E(0,
,2),C(-1,
,0).
∴
=(-1,
,2),
=(-1,0,1)(7分)
设平面AEFG的法向量为n=(x,y,z)
由
取n=(1,-
,1)(9分)
而平面ABCD的一个法向量为
=(0,0,1),(10分)
∴cos?
,n>=
=
故平面AEFG与平面ABCD所成锐二面角的大小为arccos
(13分)
∴由余弦定理,可得BD=
| 3 |
又在直平行六面体中,GD⊥平面ABCD,∴GD⊥BD
又AD∩GD=D,∴BD⊥平面ADG(5分)
(Ⅱ)以D为坐标原点,建立如图所示的空间直角坐标系D-xyz
∵∠BAE=∠GAD=45°,AB=2AD=2
则有A(1,0,0),B(0,
| 3 |
| 3 |
| 3 |
∴
| AE |
| 3 |
| AG |
设平面AEFG的法向量为n=(x,y,z)
由
|
| ||
| 3 |
而平面ABCD的一个法向量为
| DG |
∴cos?
| DG |
| ||
|
|
| ||
| 7 |
故平面AEFG与平面ABCD所成锐二面角的大小为arccos
| ||
| 7 |
点评:本题考查的知识点是二面角的平面角及求法,直线与平面垂直的判定,其中(I)的关键是证得AD⊥BD和GD⊥BD,(II)的关键是建立空间直角坐标系D-xyz,将二面角问题转化为向量夹角问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
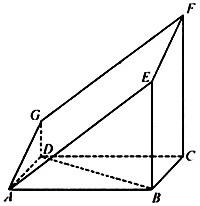
 如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°,求证:BD⊥平面ADG.
如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°,求证:BD⊥平面ADG.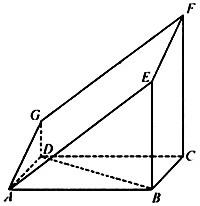 如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
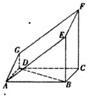
如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.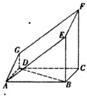 如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°,求证:BD⊥平面ADG.
如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°,求证:BD⊥平面ADG.