题目内容
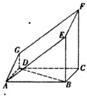如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°，求证：BD⊥平面ADG．
解：在△BAD中，∵AB=2AD=2，∠BAD=60°，
∴由余弦定理可得BD=
，∴AB2=AD2+BD2，∴AD⊥BD
又在直平行六面体中，GD⊥平面ABCD，BD?平面ABCD
∴GD⊥BD又AD∩GD=D
∴BD⊥平面ADG
分析：欲证BD⊥平面ADG，根据直线与平面垂直的判定定理可知只需证BD与平面ADG内两相交直线垂直，而根据余弦定理可得AD⊥BD
，GD⊥BD又AD∩GD=D，满足定理条件．
点评：本题主要考查了直线与平面垂直的判定，考查空间想象能力、运算能力和推理论证能力，属于常规题型．
∴由余弦定理可得BD=
，∴AB2=AD2+BD2，∴AD⊥BD又在直平行六面体中，GD⊥平面ABCD，BD?平面ABCD
∴GD⊥BD又AD∩GD=D
∴BD⊥平面ADG
分析：欲证BD⊥平面ADG，根据直线与平面垂直的判定定理可知只需证BD与平面ADG内两相交直线垂直，而根据余弦定理可得AD⊥BD
，GD⊥BD又AD∩GD=D，满足定理条件．
点评：本题主要考查了直线与平面垂直的判定，考查空间想象能力、运算能力和推理论证能力，属于常规题型．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°，求证：BD⊥平面ADG．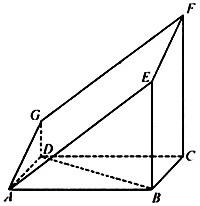
如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．
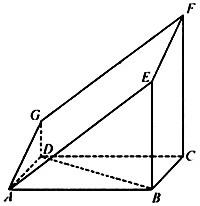如图的多面体是直平行六面体ABCD-A1B1C1D1经平面AEFG所截后得到的图形，其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．