题目内容
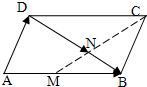如图，在平行四边形ABCD，| AD |
| AB |
| DN |
| NB |
（1）当t=2时，证明：M、N、C三点共线；
（2）若M、N、C三点共线，求实数t的值．
分析：本题考查的知识点是向量共线定理，由在平行四边形ABCD，
=a，
=b，M为AB的中点，点N在DB上，且
=t
．
（1）当t=2时，
=2
，由M为AB中点，我们易得：
=2
，又由
与
有公共点N，故M，N，C三点共线；
（2）若M、N、C三点共线，得
=λ
（λ＞0），根据ABCD为平行四边形，且M为AB的中点，我们易得到一个关于λ、t的方程，解方程后，即可求出满足条件的t值．
| AD |
| AB |
| DN |
| NB |
（1）当t=2时，
| DN |
| NB |
| NC |
| MN |
| NC |
| MN |
（2）若M、N、C三点共线，得
| NC |
| MN |
解答：证明：（1）当t=2时，
=2
，
有
=
=
(
-
)=
(b-a)，
又
+
=
，
∴
=
-
=
b-
(b-a)=
b+
a；
=
-
=
-2
=b-
(b-a)=
b+
a，
则
=2
，
与
有公共点N，
于是M、N、C三点共线；
解：（2）由
=t
，
得
=
=
(b-a)，
=
=
(b-a)，
=
-
=b-
(b-a)=
b+
a，
=
-
=
b-
(b-a)=
b+
a，
由M、N、C三点共线，得
=λ
，
∴
b+
a=
b+
a，
得
=
，且
=
，
解得t=2或t=-1（舍去）；
∴t=2．
| DN |
| NB |
有
| NB |
| 1 |
| 3 |
| DB |
| 1 |
| 3 |
| AB |
| AD |
| 1 |
| 3 |
又
| MN |
| NB |
| MB |
∴
| MN |
| MB |
| NB |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| NC |
| DC |
| DN |
| AB |
| NB |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
则
| NC |
| MN |
| NC |
| MN |
于是M、N、C三点共线；
解：（2）由
| DN |
| NB |
得
| DN |
| t |
| t+1 |
| DB |
| t |
| t+1 |
| NB |
| 1 |
| t+1 |
| DB |
| 1 |
| t+1 |
| NC |
| DC |
| DN |
| t |
| t+1 |
| 1 |
| t+1 |
| t |
| t+1 |
| MN |
| MB |
| NB |
| 1 |
| 2 |
| 1 |
| t+1 |
| t-1 |
| 2(t+1) |
| 1 |
| t+1 |
由M、N、C三点共线，得
| NC |
| MN |
∴
| 1 |
| t+1 |
| t |
| t+1 |
| λ(t-1) |
| 2(t+1) |
| λ |
| t+1 |
得
| 1 |
| t+1 |
| λ(t-1) |
| 2(t+1) |
| t |
| t+1 |
| λ |
| t+1 |
解得t=2或t=-1（舍去）；
∴t=2．
点评：若A、B、P三点共线，O为直线外一点，则
=λ
+μ
，且λ+μ=1，反之也成立，这是三点共线在向量中最常用的证明方法和性质，大家一定要熟练掌握．
| OP |
| OA |
| OB |
练习册系列答案
相关题目
如图，在平行四边形ABCD中，下列结论中错误的是（ ）A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图，在平行四边形ABCD中，
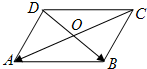如图，在平行四边形ABCD中，若
如图，在平行四边形OABC中，点O是原点，点A和点C的坐标分别是（3，0）、（1，3），点D是线段AB上的中点．