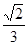题目内容
设△ABC的内角A、B、C所对的边分别为a、b、c,已知a=1,b=2,cosC=. (1)求△ABC的周长; (2)求cos(A-C)的值.
(1)∵c2=a2+b2-2abcosC=1+4-4×=4,
∴c=2,∴△ABC的周长为a+b+c=1+2+2=5.
(2)∵cosC=,∴sinC===,
∴sinA===.
∵a<c,∴A<C,故A为锐角,
∴cosA===.
∴cos(A-C)=cosAcosC+sinAsinC=×+×=.
∴c=2,∴△ABC的周长为a+b+c=1+2+2=5.
(2)∵cosC=,∴sinC===,
∴sinA===.
∵a<c,∴A<C,故A为锐角,
∴cosA===.
∴cos(A-C)=cosAcosC+sinAsinC=×+×=.
(1)借助余弦定理求出边c,直接求周长即可.(2)根据两角差的余弦公式需要求sinC,sinA,cosA,由正弦定理即可求出sinA,进而可求出cosA.sinC可由cosA求出,问题得解.

练习册系列答案
相关题目
 的内角
的内角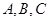 所对的边分别为
所对的边分别为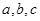 ,且
,且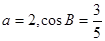 .
.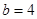 ,求
,求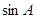 的值;
的值;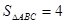 ,求
,求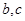 的值.
的值. ,AD=2AB,若P是平面ABCD内一点,且满足
,AD=2AB,若P是平面ABCD内一点,且满足 (
(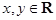 ),则当点P在以A为圆心,
),则当点P在以A为圆心, 为半径的圆上时,实数
为半径的圆上时,实数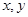 应满足关系式为( )
应满足关系式为( )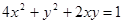

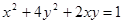
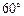 角的直线型轨道上
角的直线型轨道上 按箭头的方向运动。问:
按箭头的方向运动。问:
 中,角
中,角 所对的边分别为
所对的边分别为 .已知
.已知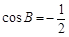 .
. . 求
. 求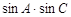 的取值范围
的取值范围 中,设内角
中,设内角 的对边分别是
的对边分别是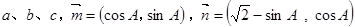 ,且
,且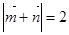
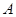 的大小;
的大小;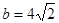 ,且
,且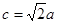 ,求
,求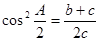 ,则△ABC是( )
,则△ABC是( )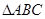 内角
内角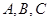 的对边分别是
的对边分别是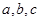 ,若
,若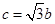 ,
,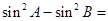
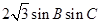 ,则
,则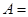 .
.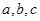 ,若
,若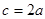 ,
,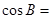 ( )
( )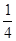 B.
B. 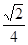 C.
C. 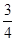 D.
D.