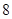题目内容
将边长为 的正方形
的正方形 沿对角线
沿对角线 折起,使得平面
折起,使得平面 平面
平面 ,在折起后形成的三棱锥
,在折起后形成的三棱锥 中,给出下列三个命题:
中,给出下列三个命题:
①面 是等边三角形; ②
是等边三角形; ② ; ③三棱锥
; ③三棱锥 的体积是
的体积是 .
.
其中正确命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
C
解析试题分析: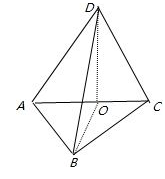
如上图所示:BD= DO=
DO= =1
=1
又BC=DC=1
∴面DBC是等边三角形①正确.∵AC⊥DO,AC⊥BO,∴AC⊥平面DOB,∴AC⊥BD,②正确.
,三棱锥D-ABC的体积=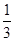 S△ABC• OD=
S△ABC• OD=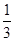
 1•1•
1•1• =
= ,③不正确.故答案为:①②,选C.
,③不正确.故答案为:①②,选C.
考点:本题主要是考查折叠问题,要注意折叠前后的改变的量和位置,不变的量和位置,属中档题.
点评:解决该试题的关键是先作出图来,①根据图可知BD,DO的值,再由BC=DC=1,可知面DBC是等边三角形.
②由AC⊥DO,AC⊥BO,可得AC⊥平面DOB,从而有AC⊥BD.

练习册系列答案
相关题目
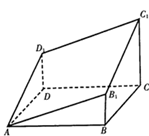
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,则下列结论中错误的是 ( )
,则下列结论中错误的是 ( )
A. |
B. |
C.三棱锥 的体积为定值 的体积为定值 |
D.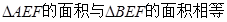 |
各棱长均为 的三棱锥的表面积为
的三棱锥的表面积为
A. | B. | C.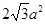 | D. |
若三棱锥的一条棱长为 ,其余棱长均为1,体积是
,其余棱长均为1,体积是 ,则函数
,则函数 在其定义域上为( )
在其定义域上为( )
| A.增函数且有最大值 | B.增函数且没有最大值 |
| C.不是增函数且有最大值 | D.不是增函数且没有最大值 |
如图,在正方体 中,
中, 为
为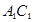 的中点,则异面直线
的中点,则异面直线 与
与 所成的角为( )
所成的角为( )
| A.30° | B.45° | C.60° | D.90 ° |


 B.
B. C.
C.  D.
D. 





 ,一个内角为
,一个内角为 的菱形,俯视图为正方形,那么这个几何体的表面积为
的菱形,俯视图为正方形,那么这个几何体的表面积为