题目内容
下列类比推理的结论正确的是( )
①类比“实数的乘法运算满足结合律”,得到猜想“向量的数量积运算满足结合律”;
②类比“平面内,同垂直于一直线的两直线相互平行”,得到猜想“空间中,同垂直于一直线的两直线相互平行”;
③类比“设等差数列{an}的前n项和为Sn,则S4,S8-S4,S12-S8成等差数列”,得到猜想“设等比数列{bn}的前n项积为Tn,则T4,
,
成等比数列”;
④类比“设AB为圆的直径,P为圆上任意一点,直线PA,PB的斜率存在,则kPA•kPB为常数”,得到猜想“设AB为椭圆的长轴,p为椭圆上任意一点,直线PA•PB的斜率存在,则kPA•kPB为常数”.
①类比“实数的乘法运算满足结合律”,得到猜想“向量的数量积运算满足结合律”;
②类比“平面内,同垂直于一直线的两直线相互平行”,得到猜想“空间中,同垂直于一直线的两直线相互平行”;
③类比“设等差数列{an}的前n项和为Sn,则S4,S8-S4,S12-S8成等差数列”,得到猜想“设等比数列{bn}的前n项积为Tn,则T4,
| T8 |
| T4 |
| T12 |
| T8 |
④类比“设AB为圆的直径,P为圆上任意一点,直线PA,PB的斜率存在,则kPA•kPB为常数”,得到猜想“设AB为椭圆的长轴,p为椭圆上任意一点,直线PA•PB的斜率存在,则kPA•kPB为常数”.
分析:
•(
•
),(
•
)•
,分别为与向量
,
共线的向量,当
,
方向不同时,向量的数量积运算结合律不成立;空间中,同垂直于一直线的两直线可能平行,可能相交,也可能异面;利用排除法可得答案.
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| c |
| a |
| c |
解答:解:
•(
•
)与向量
共线,(
•
)•
与向量
共线,
当
,
方向不同时,向量的数量积运算结合律不成立,故①错误,可排除A,B答案;
空间中,同垂直于一直线的两直线可能平行,可能相交,也可能异面,故②错误,可排除C答案;
故选D
| a |
| b |
| c |
| a |
| a |
| b |
| c |
| c |
当
| a |
| c |
空间中,同垂直于一直线的两直线可能平行,可能相交,也可能异面,故②错误,可排除C答案;
故选D
点评:本题考查的知识点是类比推理,其中利用排除法排除错误答案是解答选择题的常用技巧.

练习册系列答案
相关题目
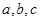 ,若
,若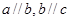 ,则
,则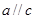 .类推出:向量
.类推出:向量 ,若
,若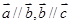 则
则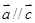
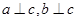 ,则
,则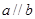 .类推出:空间中,三条不同的直线
.类推出:空间中,三条不同的直线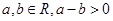 则
则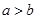 .类比出:任意
.类比出:任意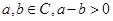 则
则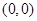 为圆心,
为圆心,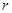 为半径的圆的方程是
为半径的圆的方程是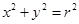 .类推出:以点
.类推出:以点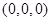 为球心,
为球心,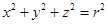
 ,若
,若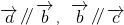 则
则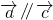 .
.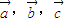 ,若
,若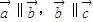 则
则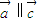 .
.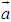 ,
,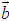 ,
,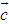 ,若
,若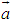 ∥
∥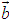 ,
,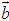 ∥
∥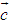 则
则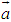 ∥
∥