题目内容
下列使用类比推理所得结论正确的序号是
(1)直线a,b,c,若a∥b,b∥c,则a∥c.类推出:向量
,
,
,若
∥
,
∥
则
∥
.
(2)同一平面内,三条不同的直线a,b,c,若a⊥c,b⊥c,则a∥b.类推出:空间中,三条不同的直线a,b,c,若a⊥c,b⊥c,则a∥b.
(3)任意a,b∈R,a-b>0则a>b.类比出:任意a,b∈C,a-b>0则a>b.
(4)以点(0,0)为圆心,r为半径的圆的方程是x2+y2=r2.类推出:以点(0,0,0)为球心,r为半径的球的方程是x2+y2+z2=r2.
(4)
(4)
.(1)直线a,b,c,若a∥b,b∥c,则a∥c.类推出:向量
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
(2)同一平面内,三条不同的直线a,b,c,若a⊥c,b⊥c,则a∥b.类推出:空间中,三条不同的直线a,b,c,若a⊥c,b⊥c,则a∥b.
(3)任意a,b∈R,a-b>0则a>b.类比出:任意a,b∈C,a-b>0则a>b.
(4)以点(0,0)为圆心,r为半径的圆的方程是x2+y2=r2.类推出:以点(0,0,0)为球心,r为半径的球的方程是x2+y2+z2=r2.
分析:本题考查的知识点是类比推理,我们根据判断命题真假的办法,对四个答案中类比所得的结论逐一进行判断,即可得到答案.
解答:解:(1)若向量
=
,则若
∥
,
∥
则
∥
不正确,故(1)错误;
(2)空间内,直线a与b可以相交、平行、异面,故(2)不正确;
(3)若a,b∈C,当a=1+i,b=i时,a-b=1>0,但a,b 是两个虚数,不能比较大小.故(3)不正确;
(4)设点P(x,y,z)是球面上的任一点,由|OP|=r,得
=r,从而球的方程是x2+y2+z2=r2.故(4)正确.
故答案为:(4).
| b |
| 0 |
| a |
| b |
| b |
| c |
| a |
| c |
(2)空间内,直线a与b可以相交、平行、异面,故(2)不正确;
(3)若a,b∈C,当a=1+i,b=i时,a-b=1>0,但a,b 是两个虚数,不能比较大小.故(3)不正确;
(4)设点P(x,y,z)是球面上的任一点,由|OP|=r,得
| x2+y2+z2 |
故答案为:(4).
点评:归纳推理与类比推理不一定正确,我们在进行类比推理时,一定要注意对结论进行进一步的论证,如果要证明一个结论是正确的,要经过严密的论证,但要证明一个结论是错误的,只需要举出一个反例.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
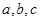 ,若
,若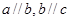 ,则
,则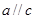 .类推出:向量
.类推出:向量 ,若
,若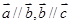 则
则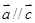
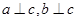 ,则
,则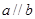 .类推出:空间中,三条不同的直线
.类推出:空间中,三条不同的直线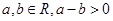 则
则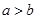 .类比出:任意
.类比出:任意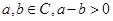 则
则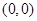 为圆心,
为圆心,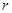 为半径的圆的方程是
为半径的圆的方程是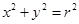 .类推出:以点
.类推出:以点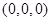 为球心,
为球心,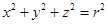
 ,若
,若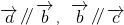 则
则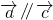 .
.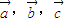 ,若
,若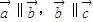 则
则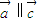 .
.