题目内容
将4名学生分配到甲、乙、丙3个实验室准备实验,每个实验室至少分配1名学生的不同分配方案共有( )
A. 种 种 | B. 种 种 | C.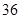 种 种 | D. 种 种 |
C
解析试题分析:先将4名学生分成三组,人数分别为2、1、1,共有 种,再讲这三组分配到3个实验室,有
种,再讲这三组分配到3个实验室,有 种,由分步计数原理,不同分配方案共有
种,由分步计数原理,不同分配方案共有 种.
种.
考点:排列和组合.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某搬运工不慎将4件次品与6件正品混在一起,由于产品外观一样,需要用仪器对产品一一检测,直至找到所有次品为止,若至多检测6次就能找到所有次品,则不同的检测方法共有( )种.
| A.1950 | B.2130 | C.7800 | D.8520 |
一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种是为( )
A. | B.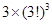 | C. | D.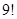 |
如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法有( )
| A.288种 |
| B.264种 |
| C.240种 |
| D.168种 |
 展开式中
展开式中 项的系数为( )
项的系数为( )
A. | B. | C. | D. |
在 的展开式中,
的展开式中, 的系数为( )
的系数为( )
A. | B. | C. | D. |
有红,蓝,黄,绿四种颜色的球各6个,每种颜色的6个球分别标有1、2、3、4、5、6,从中任取3个标号不同的球,这3个颜色互不相同且所标数字互不相邻的取法种数为( )
| A.80 | B.84 | C.96 | D.104 |
设(x- )6的展开式中x3的系数为A,二项式系数为B,则A∶B=( )
)6的展开式中x3的系数为A,二项式系数为B,则A∶B=( )
| A.4 | B.-4 | C.26 | D.-26 |
将9个相同的小球放入3个不同的盒子,要求每个盒子中至少有1个小球,且每个盒子中的小球个数都不相同,则共有不同的放法( )
| A.15种 | B.18种 |
| C.19种 | D.21种 |