题目内容
设函数
，则满足
的
的取值范围是
A． | B． | C． | D． |
D
解析试题分析：由函数可知对
与
进行讨论,即可求得满足的的取值范围
Ⅰ当时
解得
Ⅱ当
时
解得
综上
故选D
考点：函数单调性的判断与证明．
练习册系列答案
相关题目
设
，则（ ）
A． | B． | C． | D． |
= （ ）
A． | B． | C． | D． |
已知函数
为减函数，则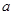
的取值范围是（ ）
A． | B． | C． | D． |
有4个命题：①对于任意
；②存在
③对于任意的
；④对于任意的
其中的真命题是（ ）
| A．①③ | B．①④ | C．②③ | D．②④ |
设
,则使函数
为奇函数的所有α值为( )
| A．1,3 | B．-1,1 | C．-1,3 | D．-1,1,3 |
对于函数
)中任意的
有如下结论：
①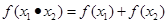
；
②
；
③
；
④
；
⑤
.
当
时，上述结论中正确结论的个数是( )
| A．2个 | B．3个 | C．4个 | D．5个 |
已知
，
，
，则
的大小关系是（ ）
A． | B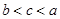． | C． | D． |
已知函数
,则
（ ）
A． | B． | C． | D． |