题目内容
11.曲线y=x2-2x与直线x=-1,x=1以及x轴所围图形的面积为( )| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
分析 先根据题意画出区域,然后依据图形利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可
解答 解:根据题意画出图形,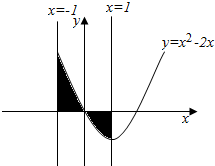
曲线y=x2-2x,与直线x=-1,x=1,以及x轴所围成的曲边梯形的面积为${∫}_{-1}^{0}({x}^{2}-2x)dx+{∫}_{0}^{1}(2x-{x}^{2})dx$=($\frac{1}{3}$x3-x2)|${\;}_{-1}^{0}$+(x2$-\frac{1}{3}$x3)|${\;}_{0}^{1}$=$\frac{4}{3}$$+\frac{2}{3}$=2;
故选:A.
点评 本题主要考查了学生会求出原函数的能力,以及考查了数形结合的思想,同时会利用定积分求图形面积的能力,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.已知在数列{an}中,a1=1,an=$\frac{{a}_{n-1}}{2{a}_{n-1}+1}$,则a12等于( )
| A. | $\frac{1}{21}$ | B. | $\frac{1}{23}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{27}$ |
6.双曲线x2-4my2=4的实轴长是虚轴长的2倍,则实数m=( )
| A. | 1 | B. | $\frac{1}{16}$ | C. | $\frac{1}{2}$ | D. | 1或$\frac{1}{16}$ |
16.某商场欲研究每天平均气温与商场空调日销量的关系,抽取了去年10月1日至5日每日平均气温与空调销量的数据,得到如下资料:
该商场确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若选取的是10月1日至2日的两组数据,请根据10月3日至10月5日的数据,求出y关于x的线性回归方程$\hat y=bx+a$;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2件,则认为得到的线性回归方程是可靠的,试问(2)中所得到的线性回归方程是否可靠?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 |
| 平均气温x(°C) | 29 | 26 | 24 | 22 | 20 |
| 销量y(件) | 11 | 8 | 7 | 5 | 3 |
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若选取的是10月1日至2日的两组数据,请根据10月3日至10月5日的数据,求出y关于x的线性回归方程$\hat y=bx+a$;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2件,则认为得到的线性回归方程是可靠的,试问(2)中所得到的线性回归方程是否可靠?
3.将圆x2+y2=1变换为椭圆$\frac{{{{x'}^2}}}{4}+\frac{{{{y'}^2}}}{9}=1$的伸缩变换公式为( )
| A. | $\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}\right.$ | B. | $\left\{\begin{array}{l}x'=3x\\ y'=2y\end{array}\right.$ | C. | $\left\{\begin{array}{l}x'=\frac{1}{2}x\\ y'=\frac{1}{3}y\end{array}\right.$ | D. | $\left\{\begin{array}{l}x'=\frac{1}{3}x\\ y'=\frac{1}{2}y\end{array}\right.$ |
1.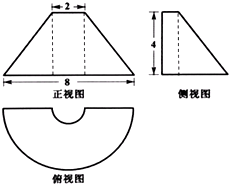 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )
 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形.则该几何体表面积等于( )| A. | 12+$\frac{47π}{2}$ | B. | 12+23π | C. | 12+24π | D. | 12+$\frac{45}{2}$π |