题目内容
与直线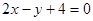 平行的抛物线
平行的抛物线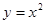 的切线方程是
的切线方程是
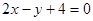 平行的抛物线
平行的抛物线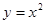 的切线方程是
的切线方程是A.2x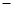 y+3=0 y+3=0 | B.2x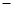 y y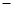 3=0 3=0 |
C.2x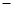 y+1=0 y+1=0 | D.2x y y 1=0 1=0 |
D
根据导数的几何意义求出函数f(x)在x处的导数等于切线的斜率,建立等式,求出x的值,从而求出切点坐标,最后将切线方程写出一般式即可.
解:y’=2x
2x=2即x=1
∴切点坐标为(1,1)
∴与直线2x-y+4=0的平行的抛物线y=x2的切线方程是 2x-y-1=0
故答案为D
解:y’=2x
2x=2即x=1
∴切点坐标为(1,1)
∴与直线2x-y+4=0的平行的抛物线y=x2的切线方程是 2x-y-1=0
故答案为D

练习册系列答案
相关题目
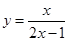 在点(1,1)处的切线方程为( )
在点(1,1)处的切线方程为( )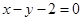
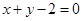
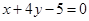
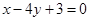
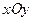 中,直线
中,直线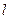 的参数方程为
的参数方程为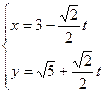 (
( 为参数),在极
为参数),在极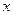 轴正半轴为极轴)中,圆C的方程为
轴正半轴为极轴)中,圆C的方程为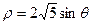 。
。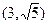 ,求|PA|+|PB|。
,求|PA|+|PB|。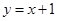 上的一点向圆
上的一点向圆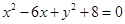 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )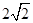
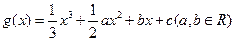 的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为
的图象经过原点,在其图象上一点P(x,y)处的切线的斜率记为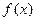 .
.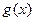 在区间[-1,3]上是单调递减函数,求
在区间[-1,3]上是单调递减函数,求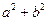 的最小值.
的最小值.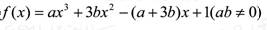 在x=1处取得极值,在x=2处的切线平行于向量
在x=1处取得极值,在x=2处的切线平行于向量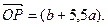
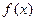 的单调区间;
的单调区间;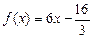 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.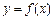 及其导函数
及其导函数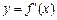 的图象如图所示,则曲线
的图象如图所示,则曲线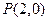 处的切线方程是
处的切线方程是 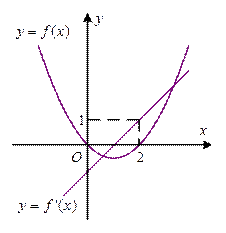

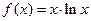 的单调递减区间是 .
的单调递减区间是 .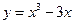 的递减区间是 .
的递减区间是 .