题目内容
在 中,若
中,若 ,
, ,则
,则 的最小值是 。
的最小值是 。
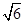
解析试题分析:根据题意,由于向量 ,且给定其向量的夹角为
,且给定其向量的夹角为 ,那么根据向量的数量积公式可知bc=2,再由余弦定理
,那么根据向量的数量积公式可知bc=2,再由余弦定理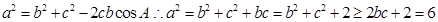 ,因此可知其长度的最小值为
,因此可知其长度的最小值为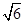 ,故填写
,故填写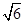 。
。
考点:本试题考查了解三角形的运用。
点评:解决该试题的关键是利用向量的数量积得到bc的乘积,然后借助于余弦定理得到a与b,c的关系式,进而运用均值不等式来得到最值,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
在 中,若
中,若 ,
, ,则
,则 的最小值是 。
的最小值是 。
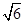
解析试题分析:根据题意,由于向量 ,且给定其向量的夹角为
,且给定其向量的夹角为 ,那么根据向量的数量积公式可知bc=2,再由余弦定理
,那么根据向量的数量积公式可知bc=2,再由余弦定理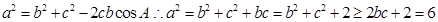 ,因此可知其长度的最小值为
,因此可知其长度的最小值为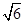 ,故填写
,故填写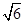 。
。
考点:本试题考查了解三角形的运用。
点评:解决该试题的关键是利用向量的数量积得到bc的乘积,然后借助于余弦定理得到a与b,c的关系式,进而运用均值不等式来得到最值,属于中档题。

 阅读快车系列答案
阅读快车系列答案