题目内容
是否存在常数 使得
使得 对一切
对一切 恒成立?若存在,求出
恒成立?若存在,求出 的值,并用数学归纳法证明;若不存在,说明理由.
的值,并用数学归纳法证明;若不存在,说明理由.

解析试题分析:先探求出 的值,即令
的值,即令 ,解得
,解得 .用数学归纳法证明时,需注意格式.第一步,先证起始项成立,第二步由归纳假设证明当n="k" 等式成立时,
.用数学归纳法证明时,需注意格式.第一步,先证起始项成立,第二步由归纳假设证明当n="k" 等式成立时,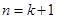 等式也成立.最后由两步归纳出结论.其中第二步尤其关键,需利用归纳假设进行证明,否则就不是数学归纳法.
等式也成立.最后由两步归纳出结论.其中第二步尤其关键,需利用归纳假设进行证明,否则就不是数学归纳法.
解:取 和2 得
和2 得 解得
解得 4分
4分
即
以下用数学归纳法证明:
(1)当n=1时,已证 6分
(2)假设当n=k, 时等式成立
时等式成立
即 8分
8分
那么,当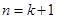 时有
时有 10分
10分 12分
12分
就是说,当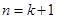 时等式成立 13分
时等式成立 13分
根据(1)(2)知,存在 使得任意
使得任意 等式都成立 15分
等式都成立 15分
考点:数学归纳法

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的前
的前 项和为
项和为 ,且满足
,且满足
 .
. ,
, ,
, ,
, 的值并写出其通项公式;
的值并写出其通项公式; ;
; 均为实数,且
均为实数,且 ,
, ,
, ,求证
,求证 都是正实数,且
都是正实数,且 .求证:
.求证: 与
与 中至少有一个成立.
中至少有一个成立. (
( )
) 均为实数,且
均为实数,且 ,
, ,
, 求证:
求证:

 ,
, <a<c+
<a<c+
