题目内容
P是双曲线 的右支上一点,F1,F2分别为双曲线的左、右焦点,焦距为2c,则△PF1F2的内切圆的圆心横坐标为( )
的右支上一点,F1,F2分别为双曲线的左、右焦点,焦距为2c,则△PF1F2的内切圆的圆心横坐标为( )A.-a
B.a
C.-c
D.c
【答案】分析:点P是双曲线右支上一点,按双曲线的定义,|PF1|-|PF2|=2a,设三角形PF1F2的内切圆心在横轴上的投影为A(x,0),B、C分别为内切圆与PF1、PF2的切点.由同一点向圆引得两条切线相等知|PF1|-|PF2|=(PB+BF1)-(PC+CF2),由此得到△PF1F2的内切圆的圆心横坐标.
解答:解:∵点P是双曲线右支上一点,
∴按双曲线的定义,|PF1|-|PF2|=2a,
若设三角形PF1F2的内切圆心在横轴上的投影为A(x,0),该点也是内切圆与横轴的切点.
设B、C分别为内切圆与PF1、PF2的切点.考虑到同一点向圆引得两条切线相等:
则有:PF1-PF2=(PB+BF1)-(PC+CF2)
=BF1-CF2=AF1-F2A
=(c+x)-(c-x)
=2x=2a
x=a
所以内切圆的圆心横坐标为a.
故选B.
点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答.
解答:解:∵点P是双曲线右支上一点,
∴按双曲线的定义,|PF1|-|PF2|=2a,
若设三角形PF1F2的内切圆心在横轴上的投影为A(x,0),该点也是内切圆与横轴的切点.
设B、C分别为内切圆与PF1、PF2的切点.考虑到同一点向圆引得两条切线相等:
则有:PF1-PF2=(PB+BF1)-(PC+CF2)
=BF1-CF2=AF1-F2A
=(c+x)-(c-x)
=2x=2a
x=a
所以内切圆的圆心横坐标为a.
故选B.
点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 的右支上一点,A1, A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为
的右支上一点,A1, A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为 ,有下列命题:
,有下列命题: ;
; ;
; 的内切圆的圆心横坐标为
的内切圆的圆心横坐标为 ;
;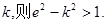
 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
 ,则e的最大值为
,则e的最大值为
 的内切圆的圆心横坐标为a;
的内切圆的圆心横坐标为a;
 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为 ;
; ;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是 .
;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是 . 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题: ;
; ;
; 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题: ;
; ;
;