题目内容
已知P是双曲线 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为
 ;
;②若|PF1|=e|PF2|,则e的最大值为
 ;
;③△PF1F2的内切圆的圆心横坐标为a;
其中正确命题的序号是 .
【答案】分析:分别求得双曲线的渐近线和准线方程,进而求得准线被它的两条渐近线所截得的线段长度判断①正确.
根据双曲线的定义可知|PF1|-|PF2|=2a=(e-1)|PF2|≥(e-1)(c-a),进而求得e的范围,判断②不正确.
设△PF1F2的内切圆的圆心为O,内切圆切PF1于A点,PF2于B点,F1F2于C点,根据双曲线的定义可知|PF1|-|PF2|=2a.进而根据|PF1|=|PA|+|AF1|,|PF2|=|PB|+|BF2|,求得C的横坐标,判断③正确.
解答:解:双曲线的渐进线为y=± x,准线方程为x=
x,准线方程为x= ,代入渐进线方程得y=±
,代入渐进线方程得y=± =
=
∴准线被它的两条渐近线所截得的线段长度为2× =
= 故①正确.
故①正确.
∵|PF1|-|PF2|=2a=(e-1)|PF2|≥(e-1)(c-a),整理得(e-1)•(e-1)≤2,解得,e≤1+ 所以e的最大值是1+
所以e的最大值是1+ ②不正确.
②不正确.
设△PF1F2的内切圆的圆心为O,内切圆切PF1于A点,PF2于B点,F1F2于C点,
因为是内切圆,所以有OA⊥PF1,OB⊥PF2,OC⊥F1F2,且PA=PB,AF1=F1C,BF2=CF2.因为OC⊥F1F2,即x轴,只要求出C点的横坐标,就等于求出了O点的横坐标.
由双曲线的性质可知
∵|PF1|-|PF2|=2a
∵|PF1|=|PA|+|AF1|,|PF2|=|PB|+|BF2|,
∴|PF1|-|PF2|=(|PA|+|AF1|)-(|PB|+|BF2|)=|CF1|-|CF2|=2a,
又∵|CF1|+|CF2|=2c,联立可得CF2=c-a,∵F2(c,0),
∴C(a,0).
∴O点横坐标就为a,故③正确.
故答案为①③
点评:本题主要考查了双曲线的应用.解题的前提是对双曲线的基本知识能综合掌握.
根据双曲线的定义可知|PF1|-|PF2|=2a=(e-1)|PF2|≥(e-1)(c-a),进而求得e的范围,判断②不正确.
设△PF1F2的内切圆的圆心为O,内切圆切PF1于A点,PF2于B点,F1F2于C点,根据双曲线的定义可知|PF1|-|PF2|=2a.进而根据|PF1|=|PA|+|AF1|,|PF2|=|PB|+|BF2|,求得C的横坐标,判断③正确.
解答:解:双曲线的渐进线为y=±
 x,准线方程为x=
x,准线方程为x= ,代入渐进线方程得y=±
,代入渐进线方程得y=± =
=
∴准线被它的两条渐近线所截得的线段长度为2×
 =
= 故①正确.
故①正确.∵|PF1|-|PF2|=2a=(e-1)|PF2|≥(e-1)(c-a),整理得(e-1)•(e-1)≤2,解得,e≤1+
 所以e的最大值是1+
所以e的最大值是1+ ②不正确.
②不正确.设△PF1F2的内切圆的圆心为O,内切圆切PF1于A点,PF2于B点,F1F2于C点,
因为是内切圆,所以有OA⊥PF1,OB⊥PF2,OC⊥F1F2,且PA=PB,AF1=F1C,BF2=CF2.因为OC⊥F1F2,即x轴,只要求出C点的横坐标,就等于求出了O点的横坐标.
由双曲线的性质可知
∵|PF1|-|PF2|=2a
∵|PF1|=|PA|+|AF1|,|PF2|=|PB|+|BF2|,
∴|PF1|-|PF2|=(|PA|+|AF1|)-(|PB|+|BF2|)=|CF1|-|CF2|=2a,
又∵|CF1|+|CF2|=2c,联立可得CF2=c-a,∵F2(c,0),
∴C(a,0).
∴O点横坐标就为a,故③正确.
故答案为①③
点评:本题主要考查了双曲线的应用.解题的前提是对双曲线的基本知识能综合掌握.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 的右支上一点,A1, A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为
的右支上一点,A1, A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为 ,有下列命题:
,有下列命题: ;
; ;
; 的内切圆的圆心横坐标为
的内切圆的圆心横坐标为 ;
;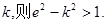
 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:
 ,则e的最大值为
,则e的最大值为
 的内切圆的圆心横坐标为a;
的内切圆的圆心横坐标为a;
 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为 ;
; ;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是 .
;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是 .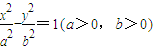 的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为
的右支上一点,A1,A2分别为双曲线的左、右顶点,F1,F2分别为双曲线的左、右焦点,双曲线的离心率为e,有下列命题:①双曲线的一条准线被它的两条渐近线所截得的线段长度为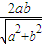 ;
;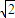 ;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是 .
;③△PF1F2的内切圆的圆心横坐标为a;④若直线PF1的斜率为k,则e2-k2>1,其中正确命题的序号是 .