题目内容
已知椭圆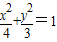 上一点P到左焦点的距离为
上一点P到左焦点的距离为 ,则它到右准线的距离为 .
,则它到右准线的距离为 .
【答案】分析:先由椭圆的第一定义求出点P到右焦点的距离,再用第二定义求出点P到右准线的距离d.
解答:解:由椭圆的第一定义得 点P到右焦点的距离等于4- =
= ,离心率e=
,离心率e= ,
,
再由椭圆的第二定义得
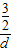 =e=
=e= ,
,
∴点P到右准线的距离d=3,
故答案为:3.
点评:本题考查椭圆的第一定义和第二定义,以及椭圆的简单性质.解题的关键是灵活利用椭圆的第二定义.
解答:解:由椭圆的第一定义得 点P到右焦点的距离等于4-
 =
= ,离心率e=
,离心率e= ,
,再由椭圆的第二定义得
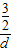 =e=
=e= ,
,∴点P到右准线的距离d=3,
故答案为:3.
点评:本题考查椭圆的第一定义和第二定义,以及椭圆的简单性质.解题的关键是灵活利用椭圆的第二定义.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
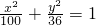 上一点P到左焦点的距离为8,则它到右准线的距离为
上一点P到左焦点的距离为8,则它到右准线的距离为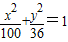 上一点P到左焦点的距离为8,则它到右准线的距离为( )
上一点P到左焦点的距离为8,则它到右准线的距离为( )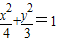 上一点P到左焦点的距离为
上一点P到左焦点的距离为 ,则它到右准线的距离为 .
,则它到右准线的距离为 .