题目内容
曲线y=-x2+4x上有两点A(4,0)、B(2,4).求:(1)割线AB的斜率kAB及AB所在直线的方程;
(2)在曲线AB上是否存在点C,使过C点的切线与AB所在直线平行?若存在,求出C点的坐标;若不存在,请说明理由.
分析:(1)直接利用两点的斜率公式即可求得割线AB的斜率,再利用直线方程的点斜式求得AB所在直线的方程即得;
(2)对于存在性问题,可先假设存在,即假设存在点C,使过C点的切线与AB所在直线平行,再利用由导函数的几何意义可知函数图象在切点处的切线的斜率值即为其点的导函数值,求得切点的坐标,结合直线的方程求出斜率等于-2的直线,若出现矛盾,则说明假设不成立,即不存在;否则存在.
(2)对于存在性问题,可先假设存在,即假设存在点C,使过C点的切线与AB所在直线平行,再利用由导函数的几何意义可知函数图象在切点处的切线的斜率值即为其点的导函数值,求得切点的坐标,结合直线的方程求出斜率等于-2的直线,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)∵点A(4,0)、B(2,4).
∴kAB=
=-2,
∴y=-2(x-4).
∴所求割线AB所在直线方程为2x+y-8=0.
(2)y′=-2x+4,-2x+4=-2,得x=3,y=-32+3×4=3.
∴C点坐标为(3,3),所求切线方程为2x+y-9=0.
故在曲线AB上存在点C,使过C点的切线与AB所在直线平行.
∴kAB=
| 4-0 |
| 2-4 |
∴y=-2(x-4).
∴所求割线AB所在直线方程为2x+y-8=0.
(2)y′=-2x+4,-2x+4=-2,得x=3,y=-32+3×4=3.
∴C点坐标为(3,3),所求切线方程为2x+y-9=0.
故在曲线AB上存在点C,使过C点的切线与AB所在直线平行.
点评:本题考查了导数的几何意义,以及直线的方程、斜率公式等基础知识,考查运算求解能力.属于基础题.本题还考查了存在性问题,所谓存在性问题,一般是要求确定满足某些特定要求的元素有或没有的问题.解题思路是:先假定所需探索的对象存在或结论成立,以此为依据进行计算或推理.

练习册系列答案
相关题目
已知a,b,c,d成等比数列,且曲线y=x2-4x的顶点是(b,c),则ad等于( )
| A、8 | B、6 | C、-8 | D、4 |
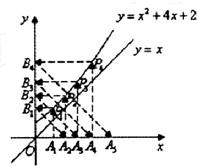 如图,过点A1作垂直于x轴的垂线交曲线y=x2+4x+2于点P1,又过点P1作x轴的平行线交y轴于点B1,记点B1关于直线y=x的对称点为A2;…;依此类推.若数列{an}的各项分别为点列An(n=1,2,3…)的横坐标,且a1=1,则an=
如图,过点A1作垂直于x轴的垂线交曲线y=x2+4x+2于点P1,又过点P1作x轴的平行线交y轴于点B1,记点B1关于直线y=x的对称点为A2;…;依此类推.若数列{an}的各项分别为点列An(n=1,2,3…)的横坐标,且a1=1,则an=