题目内容
在△ABC中,内角A,B,C所对的边分别为a,b,c,且acosB-bcosA= c,当tan(A-B)取最大值时,角C的值为( )
c,当tan(A-B)取最大值时,角C的值为( )
A.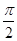
B.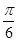
C.
D.
 c,当tan(A-B)取最大值时,角C的值为( )
c,当tan(A-B)取最大值时,角C的值为( )A.
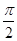
B.
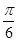
C.

D.

A
∵acosB-bcosA= c
c
∴由正弦定理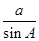 =
=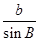 =
=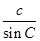
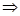 sinAcosB-sinBcosA=
sinAcosB-sinBcosA= sinC,即sin(A-B)=
sinC,即sin(A-B)= sinC
sinC
∵0〈sinC≤1
∴0<sin(A-B)≤ ,
,
在三角形ABC中,0〈A〈π,0〈B〈π
∴-π<A-B<π
∴0<A-B≤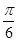 或
或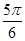 ≤A-B<π,
≤A-B<π,
又tanx在0<x≤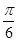 或
或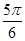 ≤x<π为增函数,且在0<x≤
≤x<π为增函数,且在0<x≤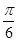 上的函数值为正,在
上的函数值为正,在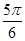 ≤x<π上的函数值为负,所以当A-B=
≤x<π上的函数值为负,所以当A-B=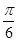 时,tan(A-B)有最大值.
时,tan(A-B)有最大值.
此时sin(A-B)= ,即sinC=1,解得C=
,即sinC=1,解得C=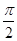 .
.
 c
c∴由正弦定理
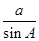 =
=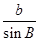 =
=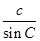
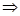 sinAcosB-sinBcosA=
sinAcosB-sinBcosA= sinC,即sin(A-B)=
sinC,即sin(A-B)= sinC
sinC∵0〈sinC≤1
∴0<sin(A-B)≤
 ,
,在三角形ABC中,0〈A〈π,0〈B〈π
∴-π<A-B<π
∴0<A-B≤
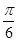 或
或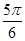 ≤A-B<π,
≤A-B<π,又tanx在0<x≤
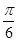 或
或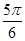 ≤x<π为增函数,且在0<x≤
≤x<π为增函数,且在0<x≤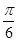 上的函数值为正,在
上的函数值为正,在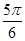 ≤x<π上的函数值为负,所以当A-B=
≤x<π上的函数值为负,所以当A-B=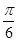 时,tan(A-B)有最大值.
时,tan(A-B)有最大值.此时sin(A-B)=
 ,即sinC=1,解得C=
,即sinC=1,解得C=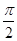 .
.
练习册系列答案
相关题目
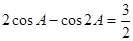
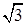 ,b+c=3,求△ABC的面积.
,b+c=3,求△ABC的面积. 中,
中, ,
,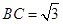 ,则
,则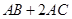 的最大值为 ;
的最大值为 ;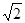 , ∠A=30°
, ∠A=30°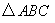 中,
中,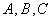 的对边分别为
的对边分别为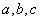 ,若
,若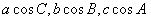 成等差数列,则
成等差数列,则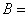 ( )
( )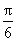
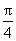
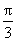
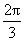
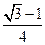 ,求C
,求C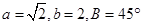 ,则角A=( )
,则角A=( )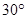 或
或
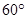 或
或
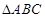 的内角
的内角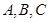 所对边的长分别为
所对边的长分别为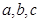 .若
.若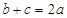 ,则
,则 则角
则角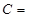 _____.
_____.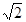 ,则c=_____
,则c=_____