题目内容
线段PQ是椭圆 过M(1,0)的一动弦,且直线PQ与直线x=4交于点S,则
过M(1,0)的一动弦,且直线PQ与直线x=4交于点S,则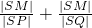 =________.
=________.
2
分析:设出直线PQ的方程,求出M,P,Q的坐标利用转化思想,求解比例的值.
解答: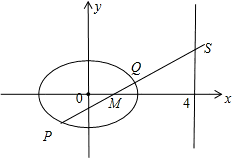 解:设直线PQ的方程为y=k(x-1),所以S(4,3k),
解:设直线PQ的方程为y=k(x-1),所以S(4,3k),
设P,Q的横坐标分别为x1,x2,
联立 解得(3+4k2)x2-8k2x+4k2-12=0,
解得(3+4k2)x2-8k2x+4k2-12=0,
所以x1+x2=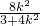
x1•x2=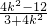 ,
,
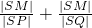 =
=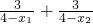
=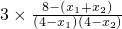
=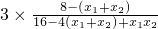
=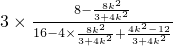
=3×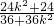
=2.
故答案为:2.
点评:本题考查椭圆的简单性质,转化思想的应用,计算能力.
分析:设出直线PQ的方程,求出M,P,Q的坐标利用转化思想,求解比例的值.
解答:
 解:设直线PQ的方程为y=k(x-1),所以S(4,3k),
解:设直线PQ的方程为y=k(x-1),所以S(4,3k),设P,Q的横坐标分别为x1,x2,
联立
 解得(3+4k2)x2-8k2x+4k2-12=0,
解得(3+4k2)x2-8k2x+4k2-12=0,所以x1+x2=
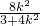
x1•x2=
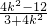 ,
,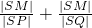 =
=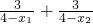
=
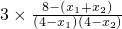
=
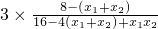
=
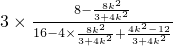
=3×
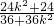
=2.
故答案为:2.
点评:本题考查椭圆的简单性质,转化思想的应用,计算能力.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
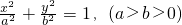 的左焦点和右焦点,O是坐标系原点,且椭圆C的焦距为6,过F1的弦AB两端点A、B与F2所成△ABF2的周长是
的左焦点和右焦点,O是坐标系原点,且椭圆C的焦距为6,过F1的弦AB两端点A、B与F2所成△ABF2的周长是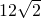 .
.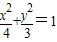 过M(1,0)的一动弦,且直线PQ与直线x=4交于点S,则
过M(1,0)的一动弦,且直线PQ与直线x=4交于点S,则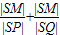 = .
= .