题目内容
在△ABC中,a=2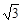 ,b=2
,b=2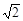 ,∠B=45°,则∠A为 ( )
,∠B=45°,则∠A为 ( )
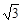 ,b=2
,b=2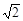 ,∠B=45°,则∠A为 ( )
,∠B=45°,则∠A为 ( )| A.30°或150° | B.60° | C.60°或120° | D.30° |
C
分析:由B的度数求出sinB的值,再由a与b的值,利用正弦定理求出sinA的值,由a大于b,根据大边对大角,得到A大于B,由B的度数及三角形内角可得出角A的范围,利用特殊角的三角函数值即可得到A的度数.
解答:解:由a=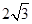 ,b=
,b=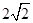 ,B=45°,
,B=45°,
根据正弦定理 =
=
得:sinA=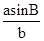 =
=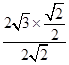 =
=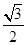 =
=
由a>b,得到A∈(45°,180°),
则角A=60°或120°.
故选C
点评:此题属于解三角形的题型,涉及的知识有正弦定理,以及特殊角的三角函数值,学生做题时注意角度的范围及三角形内角和定理这个隐含条件.
解答:解:由a=
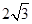 ,b=
,b=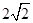 ,B=45°,
,B=45°,根据正弦定理
 =
=
得:sinA=
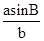 =
=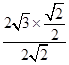 =
=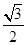 =
=由a>b,得到A∈(45°,180°),
则角A=60°或120°.
故选C
点评:此题属于解三角形的题型,涉及的知识有正弦定理,以及特殊角的三角函数值,学生做题时注意角度的范围及三角形内角和定理这个隐含条件.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 中,
中, ,
, ,
, ,则
,则 ( )
( )



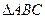 中,
中,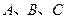 的对边分别为
的对边分别为
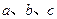 ,且
,且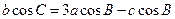 .
. 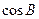 的值;
的值;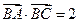 ,
,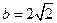 ,求
,求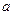 和
和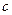 .
.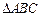 中, a,b,c分别是A、B、C的对边,且
中, a,b,c分别是A、B、C的对边,且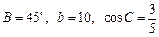 .
.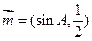 与
与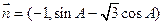 共线,其中A是△ABC的内角。
共线,其中A是△ABC的内角。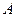 的大小; (2)若
的大小; (2)若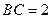 ,求
,求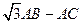 的最大值。
的最大值。 中,内角
中,内角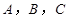 的对边分别是
的对边分别是 ,若
,若 ,
, ,则
,则 .
. ,那么BC= ___
,那么BC= ___  b=
b= ,则a、b的等比中项为
,则a、b的等比中项为