题目内容
定义新运算“&”与“*”:x&y=xy-1,x*y=log(x-1)y,则函数f(x)=
是( )
| (x&3)+1 |
| 3*2x |
分析:根据新定义求得 3*2x=log22x=x,x&3=x2,代入要求的式子化简可得函数f(x)=
,由此得出结论
| x2+1 |
| x |
解答:解:∵新运算“&”与“*”:x&y=xy-1,x*y=log(x-1)y,
∴3*2x=log22x=x,x&3=x2.
∴函数f(x)=
=
,故定义域为{x|x≠0},关于原点对称,
再由f(-x)=-
=-f(x),可得函数f(x)是奇函数.
故选A.
∴3*2x=log22x=x,x&3=x2.
∴函数f(x)=
| (x&3)+1 |
| 3*2x |
| x2+1 |
| x |
再由f(-x)=-
| x2+1 |
| x |
故选A.
点评:本题主要考查分数指数幂的运算法则的应用,对数的运算性质,属于基础题.

练习册系列答案
相关题目
定义新运算“&”与“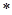 ”:
”: ,
,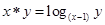 ,则函数
,则函数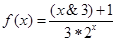
是( )
| A.奇函数 | B.偶函数 | C.非奇非偶函数 | D.既是奇函数又是偶函数 |
 ”:
”: ,
,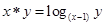 ,则函数
,则函数
 ”:
”: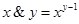 ,
, ,则函数
,则函数
 是( )
是( )