Question

PA、PB、PC是从P点出发的三条射线，每两条射线的夹角均为60°，那么直线PC与平面PAB所成角的余弦值是（　　）

• A．

  1

  2

• B．

  2

  2

• C．

  3

  3

• D．

  6

  3

Answer 1

分析：过PC上任意一点D作DO⊥平面APB，则∠DPO就是直线PC与平面PAB所成的角．先证明点O在∠APB的平分线上，通过解直角三角形PED、DOP，求出直线PC与平面PAB所成角的余弦值．

解答：解：在PC上任取一点D并作DO⊥平面APB，则∠DPO就是直线PC与平面PAB所成的角．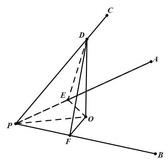         
过点O作OE⊥PA，OF⊥PB，因为DO⊥平面APB，则DE⊥PA，DF⊥PB．
△DEP≌△DFP，∴EP=FP，∴△OEP≌△OFP，
因为∠APC=∠BPC=60°，所以点O在∠APB的平分线上，即∠OPE=30°．
设PE=1，∵∠OPE=30°∴OP=

1

cos30°

=

2 3

3

在直角△PED中，∠DPE=60°，PE=1，则PD=2．
在直角△DOP中，OP=

2 3

3

，PD=2．则cos∠DPO=

OP

PD

=

3

3

．
即直线PC与平面PAB所成角的余弦值是

3

3

．
故选C．

点评：本题考查了直线与平面所成角的大小计算．解题过程构造了解题必需的直角三角形．考查空间想象能力，计算能力、转化能力．