题目内容
将4名新来的同学分配到A、B、C三个班级中,每个班级至少安排1名学生,其中甲同学不能分配到A班,那么不同的分配方案方法种数为______________(用数字作答).
24
解析试题分析:甲同学不能分配到A班,则甲可以放在B、C班,有A21种方法,
另外三个同学有2种情况,
①、三人中,有1个人与A共同分配一个班,即A、B、C每班一人,即在三个班级全排列A33,
②三人中,没有人与甲共同参加一个班,这三人都被分配到甲没有分配的2个班,
则这三中一个班1人,另一个班2人,可以从3人中选2个为一组,与另一人对应2个班,进行全排列,有C32A22种情况,
另外三个同学有A33+C32A22种安排方法,
∴不同的分配方案有A21(A33+C32A22)=24,
故答案为24.
考点:简单的排列组合应用问题
点评:中档题,特殊元素、特殊位置问题,往往从“特殊”考虑起分类讨论。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 满足
满足 ,则数组
,则数组 可能是 .
可能是 . 的分布列如下表.若
的分布列如下表.若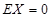 ,
, ,则
,则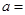 ,
, .
.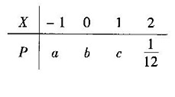
 的常数项为 .(用数字作答)
的常数项为 .(用数字作答)  的展开式中,含
的展开式中,含 的项的系数是 .
的项的系数是 . 中任取三个数字,组成无重复数字的三位数中,偶数的个数是 (用数字回答).
中任取三个数字,组成无重复数字的三位数中,偶数的个数是 (用数字回答). -
- )6的二项展开式中的常数项为_____.(用数字作答)
)6的二项展开式中的常数项为_____.(用数字作答) 的展开式中,含
的展开式中,含 的项的系数是 .
的项的系数是 .