题目内容
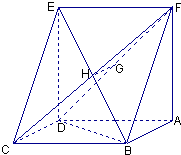
【题目】如图，四边形ABCD和ADPQ均为正方形，他们所在的平面互相垂直，动点M在线段PQ上，E，F分别为AB，BC的中点，设异面直线EM与AF所成的角为θ，则cosθ的最大值为 ．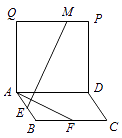 
【答案】
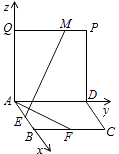
【解析】解：根据已知条件，AB，AD，AQ三直线两两垂直，分别以这三直线为x，y，z轴，建立如图所示空间直角坐标系，设AB=2，则：
A（0，0，0），E（1，0，0），F（2，1，0）；
M在线段PQ上，设M（0，y，2），0≤y≤2；
∴ 
；
∴cosθ= 
= 
；
设f（y）= ， 
；
函数g（y）=﹣2y﹣5是一次函数，且为减函数，g（0）=﹣5＜0；
∴g（y）＜0在[0，2]恒成立，∴f′（y）＜0；
∴f（y）在[0，2]上单调递减；
∴y=0时，f（y）取到最大值 ．
故答案为： ．
首先以AB，AD，AQ三直线为x，y，z轴，建立空间直角坐标系，并设正方形边长为2，M（0，y，2），从而可求出向量 
的坐标，由cosθ= 得到 
，对函数 
求导，根据导数符号即可判断该函数为减函数，从而求出cosθ的最大值．
亮点激活精编提优100分大试卷系列答案
【题目】甲、乙两所学校高三年级分别有1 200人，1 000人，为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：
甲校：
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 3 | 4 | 8 | 15 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | x | 3 | 2 |
乙校：
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 8 | 9 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 3 |
则x，y的值分别为（ ）
（A）、12,7 （B）、 10,7 （C）、 10，8 （D）、 11,9
