题目内容
（09年丹阳高级中学一摸）棱长为1的正方体
中,若E、G分别为
、
的中点,F是正方形
的中心,则空间四边形BGEF在正方体的六个面内射影的面积的最大值为 。
答案：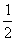
练习册系列答案
全程金卷系列答案
相关题目
全程金卷系列答案题目内容
（09年丹阳高级中学一摸）棱长为1的正方体中,若E、G分别为、的中点,F是正方形的中心,则空间四边形BGEF在正方体的六个面内射影的面积的最大值为 。
全程金卷系列答案
，其中
是自然常数，
(1)讨论
时, 
的单调性、极值；
；
，使
中，
且点
在直线
上。
(1)求数列
的通项公式;
求函数
的最小值；
表示数列
的前
项和。试问：是否存在关于
，使得
对于一切不小于2的自然数
的离心率为
，直线
与以原点为圆心、椭圆
的短半轴长为半径的圆相切。
(1)求椭圆
，右焦点为
，直线
过点
垂直于直线
,线段
的垂直平分线交
，求点
的方程；
轴交于点
，不同的两点
在
，求
的取值范围。
元（
(e为自然对数的底数)成反比例。已知每件产品的日售价为40元时，日销售量为10件。
(1)求该商店的日利润L（x）元与每件产品的日售价x元的函数关系式；
,其中向量
，
(1)求
的最小正周期；
中，
分别是角
的对边，
求
的值。