题目内容
已知函数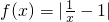
(1)由函数 的图象经过怎样的变换可以得到函数y=f(x)的图象?请作出y=f(x)的图象;
的图象经过怎样的变换可以得到函数y=f(x)的图象?请作出y=f(x)的图象;
(2)若存在实数a,b(a<b),使得集合{y|y=f(x),a≤x≤b}=[ma,mb],求实数m的取值范围.
 解:(1)将函数
解:(1)将函数 的图象向下平移一个单位,再把所得的图象在x轴下方的部分关于x轴对称,就可得到函数y=f(x)的图象.…(3分)
的图象向下平移一个单位,再把所得的图象在x轴下方的部分关于x轴对称,就可得到函数y=f(x)的图象.…(3分)(2)由题意知a<b,ma<mb,
∴m>0.
又∵f(x)≥0,
∴ma≥0.而a≠0,
∴a>0,
∴ma>0…(8分)
当0<a<b≤1时,
则
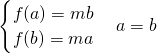 矛盾…(9分)
矛盾…(9分)当0<a<1<b时,
∵f(1)=0∉[ma,mb]矛盾…(10分)
当1≤a<b时,则
 即
即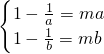
∴
 ,即mx2-x+1=0在[1,+∞)上有两个不等根
,即mx2-x+1=0在[1,+∞)上有两个不等根记g(x)=mx2-x+1,则
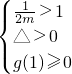 解得
解得 …(14分)
…(14分)答:所求参数m的取值范围是

分析:(1)由函数 解析式知,可将函数
 的图象向下平移一个单位,再把所得的图象在x轴下方的部分关于x轴对称得到函数
的图象向下平移一个单位,再把所得的图象在x轴下方的部分关于x轴对称得到函数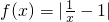 的图象;
的图象;(2)由题设条件存在实数a,b(a<b),使得集合{y|y=f(x),a≤x≤b}=[ma,mb],及函数的图象可以判断出m>0,a>0再分三类对m的取值范围进行讨论,即0<a<b≤1,0<a<b≤1,1≤a<b三类,在每一类中确定出函数的最值,将其转化为方程,分别解出符合条件的m的范围,即可得到实数m的取值范围.
点评:本题考查函数与方程的综合运用,考查函数图象的变化,集合相等的意义,函数的值域概念,解题的关键理解题意,分类转化研究参数的取值范围本题考查了分类计件思想、方程的思想,转化的思想,考查了判断推理的能力,分类讨论的技巧

练习册系列答案
相关题目
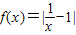
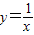 的图象经过怎样的变换可以得到函数y=f(x)的图象?请作出y=f(x)的图象;
的图象经过怎样的变换可以得到函数y=f(x)的图象?请作出y=f(x)的图象;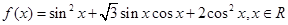 .
. ,
, 。
。

 图像经过怎样的变换得到。
图像经过怎样的变换得到。
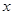 的集合;
的集合;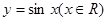 的图象经过怎样的变化而得到的
的图象经过怎样的变化而得到的