题目内容
| |||||||||||
解析:
(1) |
解析:由f(x)为奇函数易知c=0. 又因为a>0,b是自然数,所以当x<0时.f(x)<0;当x>0时,f(x)>0.所以f(x)的最大值 当x>0时f(x)= 所以 又f(1)> 所以f(x)= |
(2) |
方法一 假设存在满足条件的直线l,则P、Q的坐标可为P(x0,y0)、Q(2-x0,-y0),且这两点都在函数f(x)= 消去y0得 解得x0=1± 所以p(1+ 所以,直线l的方程为x-4y-1=0. 直线l的存在性还需通过充分性的检验. 把直线l的方程与函数y=f(x)= 因此,直线l与y=f(x)的图象共有三个交点,与“只交于两点”矛盾.所以,满足条件的直线,l不存在. 在得到这样的解答之后,我们不妨回头再看一看,在上述过程中,函数.f(x)的性质(如奇偶性)并没有得到充分的应用.若能充分运用这个已知条件,则 可以得到共他不同的探索过程. 方法二 设P(x1·y1)、Q(x2·y2),则由f(x)为奇函数可知:P关于原点的对称点 又y1+y2=0,x1+x2=2.所以| 是否存在直线m∶y=b.使得直线m与y=f(x)的图象有两个距离为2的交点. 将m∶y=b代入y= 解得x1x2= 令|x1-x2|=2. 解得b= 所以P 充分性的检验过程同上. 以上两种解法都是从求出直线的方程入手.如果我们将着眼点放在“只交于两点”,则可以得到下面简洁的解法. 方法三:当直线l的斜率不存在时.l∶x=1,此时l与函数f(x)的图象只交于一点,不满足题设,所以.可设直线PQ的方程为y=kx+b. 与y= kx3+bx2+(k-1)x+b=0( 由P、Q关于点(1,0)对称,可得点(1,0)在直线PQ上,所以b=-k.对于上述方程( 若k≠0,则方程( 点评:本题考查探索性在函数中的应用.而敏锐的观察、丰富的想像,是进行有效探索的法宝. |

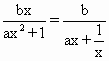 ≤
≤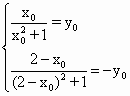
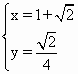
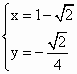
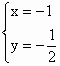
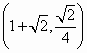 ,Q
,Q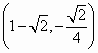 ,此时直线的方程为x-4y-1=0
,此时直线的方程为x-4y-1=0 sinx在[0,π]上的大致图象是( )
sinx在[0,π]上的大致图象是( )


 )x-1.
)x-1.